Realizando um teste qui-quadrado para independência Nos exercícios 13 a 22, realize o teste qui-quadrado para independência indicado fazendo o seguinte:
(a) Identifique a afirmação e declare H0 e Ha .
(b) Determine os graus de liberdade e o valor crítico e identifique a região de rejeição.
(c) Calcule a estatística de teste qui-quadrado. Se for conveniente, use tecnologia.
(d) Decida se rejeita ou não a hipótese nula.
(e) Interprete a decisão no contexto da afirmação original.
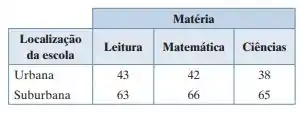
Conquistas e localização da escola A tabela de contingência a seguir mostra os resultados de uma amostra aleatória de estudantes, que atingiram níveis básicos de habilidade em três matérias, distribuídos em função da localização da escola. Com a = 0,01, teste a hipótese de que as variáveis são independentes. (Adaptado de: HUD State of the Cities Report.)
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos lá, começando pela letra (a):
Nesse exercício iremos avaliar se existe dependência entre as variáveis localização da escola e matéria acadêmica. Para isso, precisamos definir as hipóteses nula e alternativa .
Passo 2
Show, vamos para a letra (b). Para determinar o valor crítico e identificar a região de rejeição é necessário entrar o grau de liberdade e o nível de significância do teste.
O nível de significância foi dado no enunciado:
Agora precisamos determinar o grau de liberdade. No caso, ele é de acordo com o número de linhas e o número de colunas:
Logo, teremos:
Com o nível de significância de 1% e 2 graus de liberdade, o valor crítico será e a região crítica será .
Passo 3
Beleza, agora vamos para a letra (c):
Aqui vamos calcular a frequência esperada para cada célula na tabela. Para isso, vamos usar a fórmula
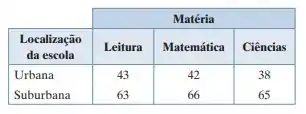
Se a gente pegar a nossa tabela,
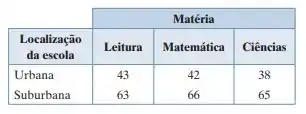
Vamos começar a calcular cada uma:
Passo 4
A estatística de teste será calculada com as frequências esperadas calculadas no Passo 3 e observadas que estão presentes na tabela.
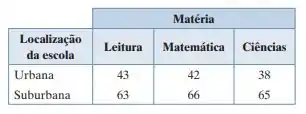
Vamos calcular usando a fórmula:
Usando a frequência esperada calculada com o valor da tabela de acordo com a coordenada da frequência esperada, somando tudo vamos encontrar:
Portanto, a estatística de teste resulta em .
Passo 5
Show, vamos para a letra (d):
Para rejeitar ou não a hipótese nula, é preciso verificar se a estatística de teste se encontra dentro da região de rejeição. Como:
Como podemos ver, , logo a hipótese nula não deve ser rejeitada.
Passo 6
Por fim, vamos para a letra (e):
Podemos afirmar que existem evidências de que as variáveis localização da escola e matéria são independentes, ou seja, uma não influencia na outra.