Reconsidere a situação descrita no Exercício 32 da Seção 8.2, e utilize o teste de Wilcoxon para testar a hipótese relevante.
Passo 1
E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:
Reconsidere a situação descrita no Exercício 32 da Seção 8.2, e utilize o teste de Wilcoxon para testar a hipótese relevante.
Testamos vs. .. A estatística de teste é s_+=soma dos ranks associados aos valores positivos de e rejeitamos no nível de significância 0,05 se s_+≥64. (da Tabela A.13, n=12, com α/2=.026, que está próximo do valor desejado de .025), ou se
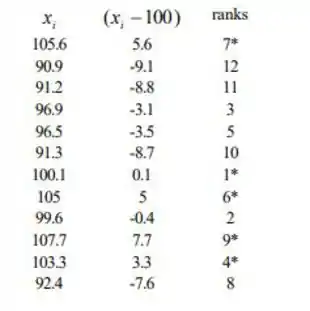
, e como 27 não é ≥64 nem ≤14, não rejeitamos . Não há evidências suficientes para sugerir que a média seja algo diferente de 100 .
Resposta
Não há evidências suficientes para sugerir que a média seja algo diferente de 100 .
Espero que tenham aprendido com essa questão, até a próxima!