Suponha que as observações são feitas em um processo nos instantes . Com base nesses dados, desejamos testar
: os constituem uma seqüência distribuída independente e identicamenteversus
Suponha que os são classificados de 1 até . Então quando é verdadeira, postos mais altos tendem a ocorrer no fim da sequiência, ao passo que se é verdadeira, postos grandes e pequenos tendem a ocorrer ao mesmo tempo. Seja a classificação de e considere o teste estatístico . Então os valores pequenos de dão suporte a (por exemplo, portanto deveria ser rejeitada em favor de se . Quando é verdadeira, qualquer sequência de postos tem probabilidade !. Utilize isto a fim de encontrar para o qual o teste tem um nível o mais próximo de 0,10 quanto possível no caso de . [Sugestāo: Liste as seqüências de classificação de 4!, calcule para cada uma e então obtenha a distribuição nula de . Veja o livro de Lehmann (na Bibliografia) para obter mais informações.]
Passo 1
E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:
Então os valores pequenos de dão suporte a (por exemplo, portanto deveria ser rejeitada em favor de se . Quando é verdadeira, qualquer sequência de postos tem probabilidade !. Utilize isto a fim de encontrar para o qual o teste tem um nível o mais próximo de 0,10 quanto possível no caso de .
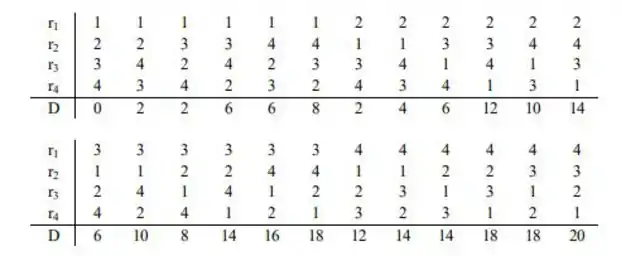
Quando é verdadeiro, cada uma das 24 sequências de classificação acima é igualmente provável, o que produz a distribuição de D quando é verdadeiro, conforme descrito na seção de resposta (por exemplo, P(D=2)=P(1243 ou 1324 ou 2134) =3/24). Então c=0 produz α=1/24=.042 enquanto c=2 implica α=4/24=.167
Resposta
Então c=0 produz α=1/24=.042 enquanto c=2 implica α=4/24=.167
Espero que tenham aprendido com essa questão, até a próxima !