A tabela abaixo mostra o índice médio de poluição num bairro de uma cidade, nos 10 primeiros meses do corrente ano. Adaptando-se uma escala de tempo conveniente e calculando-se os somatórios necessários ao cálculo da regressão, obtivemos:
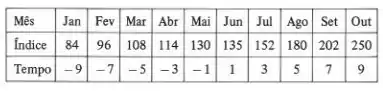
Pede-se:
a) dar a equação da regressão linear simples que se adapta aos dados;
b) interpretar os valores dos parâmetros que aparecem na equação acima;
c) dar a equação da regressão parabólica que se adapta aos dados;
d) calcular o coeficiente de explicação dessas duas regressões;
e) testar a existência de regressão parabólica e efetuar a análise do melhoramento, em relação a regressão linear, ambas ao nível de
f) estimar o índice para o mês de novembro desse mesmo ano.
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro do Mauri guerra de estática indutiva dada A tabela abaixo mostra o índice médio de poluição num bairro de uma cidade, nos 10 primeiros meses do corrente ano. Adaptando-se uma escala de tempo conveniente e calculando-se os somatórios necessários ao cálculo da regressão, obtivemos:
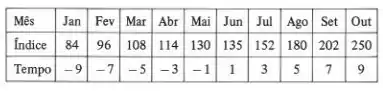
Pede-se:
a) dar a equação da regressão linear simples que se adapta aos dados;
b) interpretar os valores dos parâmetros que aparecem na equação acima;
c) dar a equação da regressão parabólica que se adapta aos dados;
d) calcular o coeficiente de explicação dessas duas regressões;
e) testar a existência de regressão parabólica e efetuar a análise do melhoramento, em relação a regressão linear, ambas ao nível de
f) estimar o índice para o mês de novembro desse mesmo ano.

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Na letra (a) para definir a regressão linear simples como,
Na letra (b) para interpretar os valores do parâmetro vamos ficar com,
Na letra ( c ) para determinar a equação da regressão parabólica temos,
Já na letra (d) para calcular o coeficiente de explicação dessas duas regressões temos,
Na letra (e) dado o nível de na regressão parábola podemos dizer que existe um melhoramento significativo
Existe um melhoramento significativo
E por fim na letra (f) estimando o índice do mês de novembro temos,
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.

Resposta
a)
b)
c)
d)
e) Existe um melhoramento significativo
f)