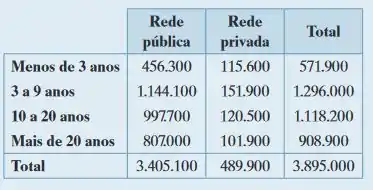
A tabela a seguir mostra os resultados de uma pesquisa na qual 3.405.100 professores da rede pública e 489.900 professores da rede privada foram questionados sobre sua experiência no ensino em tempo integral. (Adaptado de: U.S. National Center for Educations Statistics.)
a) Calcule a probabilidade de que um professor da rede privada selecionado aleatoriamente tenha de 10 a 20 anos de experiência no ensino em tempo integral.
(b) Calcule a probabilidade de que um professor selecionado aleatoriamente seja da rede pública, dado que ele tem de 3 a 9 anos de experiência no ensino em tempo integral.
(c) Os eventos “ser professor da rede pública” e “ter mais de 20 anos de experiência no ensino em tempo integral” são independentes? Explique.
(d) Qual a probabilidade de que um professor selecionado aleatoriamente tenha entre 3 e 9 anos de experiência no ensino em tempo integral ou esteja na rede privada?
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A regra da adição geral para dois eventos é dada por
A - Na tabela dada, notamos que existem 489.900 professores de escolas particulares, dos quais 120.500 professores têm 10 a 20 anos de experiência docente em tempo integral. A probabilidade é o número de resultados favoráveis dividido pelo número de resultados possíveis.
Simplificando os termos,
O que nos dá aproximadamente
Passo 2
B - Na tabela dada, notamos que existem 3405100 professores de escolas públicas de que 1144100 professores têm de 3 a 9 anos de experiência de ensino em tempo integral.
A probabilidade é o número de resultados favoráveis dividido pelo número de possíveis resultados:
Simplificando a probabilidade, nós temos que
Passo 3
C - Na tabela dada, notamos que existem 3405100 professores de escolas públicas de que 807000 professores com mais de 20 anos de experiência de ensino em tempo integral.
A probabilidade é o número de resultados favoráveis dividido pelo número de possíveis resultados:
No entanto, notamos também que 908900 dos 3895000 professores da tabela têm mais de 20 anos de experiência.
Se "ser professor de escola pública" e "ter mais de 20 anos de experiência" são independentes, então as probabilidades e devem ser iguais. Como as probabilidades são desiguais, eventos não são independentes.
Passo 4
D - Na tabela dada, notamos que existem 1296000 dos 3895000 professores tem 3 a 9 anos de experiência. A probabilidade é o número de resultados favoráveis dividido pelo número de possíveis resultados:
Observamos que 489900 dos 3895000 professores lecionam em escola particular
Observamos também que 151900 dos 3895000 professores lecionam em escola particular e
tem 3 a 9 anos de experiência.
Usando a regra da adição de forma geral
Substituindo os termos
Simplificando os termos, nós obtemos o seguinte resultado