Transformações para alcançar linearidade
Quando um modelo linear não é apropriado para representar os dados, outros modelos podem ser usados. Em alguns casos, os valores de x e y devem ser transformados para encontrar um modelo apropriado. Em uma transformação logarítmica, os logaritmos das variáveis são usados para construir o diagrama de dispersão e calcular a reta de regressão.
Nos exercícios 37 a 40, use os dados apresentados na tabela a seguir, que mostra o número de bactérias presentes após certo número de horas.
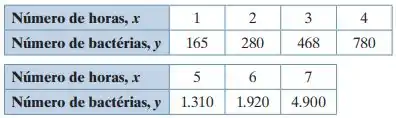
Substitua cada valor de y na tabela por seu logaritmo, log y. Encontre a equação da reta de regressão para os dados transformados. Depois, construa um diagrama de dispersão de (x, log y) com a reta de regressão, juntamente. O que você percebe?
Passo 1
E aí pessoal, belezinha. Avançando os conceitos com mais questões de regressão linear. Para começarmos, vamos obter uma nova tabela com as colunas x e log y. Para simplificar o processo de resolução, vamos continuar usando o Microsoft Excel.
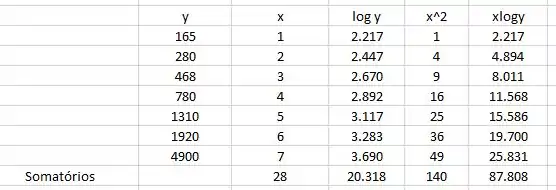
Para obtermos a equação da reta de regressão, , usamos a formulação:
Com a troca da coluna y por log y, e sabendo que a quantidade de dados é n = 7, teremos:
e
Logo, a equação da reta obtida é:
Passo 2
Após a seleção das colunas dos dados desejados, e a inserção e formatação do gráfico de dispersão (Ver exercício 17 da seção 9.2), teremos:
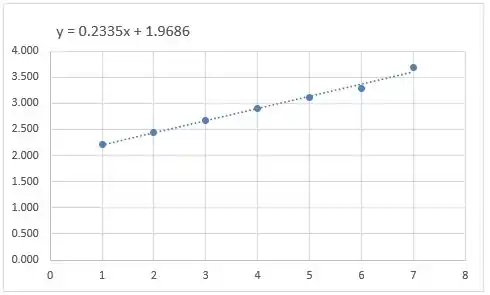
É facilmente notável a linearização dos dados, obtendo uma reta de regressão mais apropriada que a obtida no exercício anterior.
Resposta
Ver passo a passo.