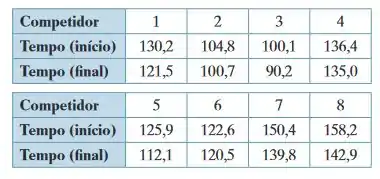
Trilha de obstáculos - Em um programa de televisão, oito competidores tentam perder o maior percentual de peso a fim de ganhar um prêmio em dinheiro. Como parte do programa, os competidores são cronometrados ao seguirem uma trilha de obstáculos. A tabela a seguir mostra os tempos (em segundos) dos competidores no início e no final da temporada. Para , há evidência suficiente para suportar a afirmação de que os tempos dos competidores mudaram?
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Primeiro, vamos tabelar os valores,
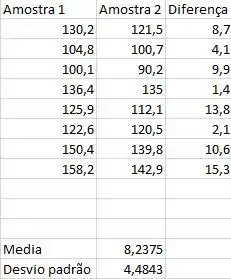
Com isso, nós temos os seguintes parâmetros:
Passo 2
A – Vamos garantir a seguinte hipótese
B – O valor crítico é o valor dado na tabela 5 com a coluna com grau de liberdade e a coluna sendo (duas caudas), logo
A região de rejeição contém todos os valores menores que e todos os valores maiores que .
C – Nós já temos o resultado pela tabela, logo
D – Determinando o valor do teste estatístico,
Substituindo os valores, nós temos que
O que nos dá aproximadamente
E – Se o valor do teste estatístico está na região de rejeição, então a hipótese nula é rejeitada!
F – Há evidência suficiente para apoiar a alegação.
Resposta
Respondido acima!