Usando distribuições normais
Nos exercícios 31 a 38, responda às questões sobre a distribuição normal especificada.
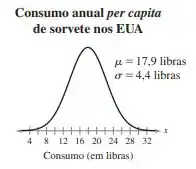
Sorvete
O consumo anual per capita de sorvete (em libras) nos Estados Unidos pode ser aproximado por uma distribuição normal, como pode ser visto na figura. (Adaptado de: U.S. Department of Agriculture.)
(a) Qual é o maior consumo anual per capita de sorvete que pode estar no grupo dos 10% que menos consomem?
(b) Entre quais dois valores encontram-se os 80% dos consumos centrais?
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos lá, começando pela letra (a).
Primeiramente, precisamos determinar o escore-z correspondente à (10º percentil), ou seja, é um valor correspondente à uma área de 0,10 à esquerda de z. Lembrando que queremos esse valor pois pretendemos encontrar o maior consumo anual per capita que ainda está dentro dos que menos consomem.
Vamos verificar na tabela:
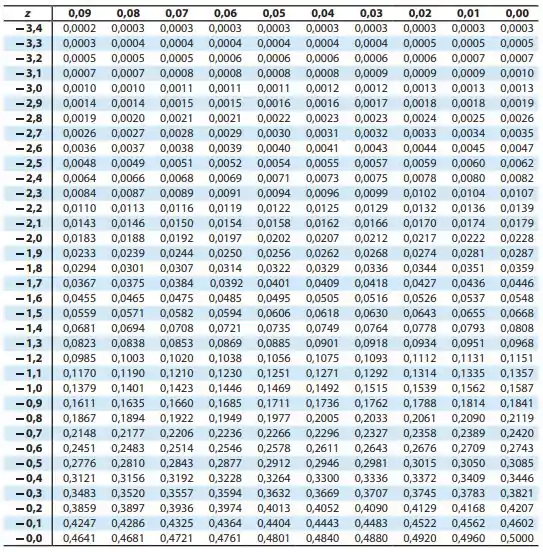
Se a gente for olhar na tabela, vamos verificar que o valor de não tem na tabela. Contudo, o valor está próximo de , então vamos considerar o escore-z iguais:
Show, com o escore-z calculado, vamos calcular o maior consumo anual per capita que ainda está dentro dos 10% que menos consomem:
Passo 2
Agora vamos para a (b):
Agora, precisamos ter em mente que desejamos determinar dois valores de escores-z que limitam 80% da área central. Logo, vamos pegar a região que vai de .
Show, com isso, vamos olhar na tabela o escore-z do valor da área mais próximo de 0,10:
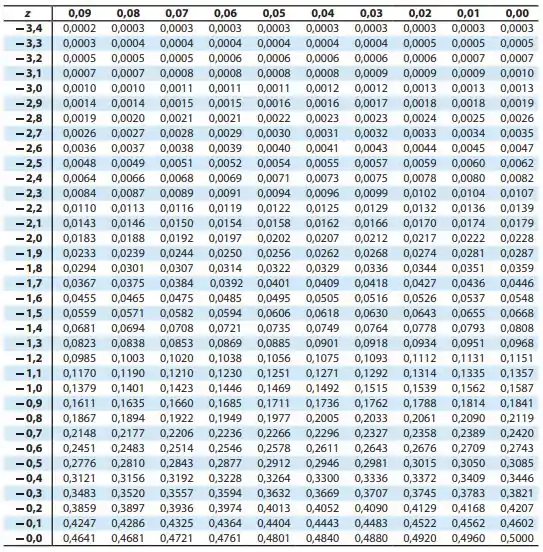
Se a gente for olhar na tabela, vamos verificar que o valor de não tem na tabela. Contudo, o valor está próximo de , então vamos considerar o escore-z iguais:
Para basta inverter o sinal:
Show, com o escore-z calculado, vamos calcular o maior consumo anual per capita para :
Agora vamos calcular o maior consumo anual per capita para :