Use regiões de rejeição para testar a afirmação sobre a média da população ao nível de significância . Suponha que a população é normalmente distribuída. Se for conveniente, use tecnologia.
Afirmação: ; ;
Estatísticas amostrais: ; .
Passo 1
Olá pessoal, vem resolver esse exercício comigo, que irei te ajudar!
Como o desvio padrão populacional () é conhecido e a população está normalmente distribuída, podemos identificar as hipóteses nula e alternativa:
O nível de significância é e a estatística de teste padronizada é:
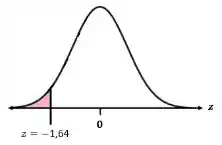
Passo 2
Com esse valor de , obtemos a área pela Tabela da distribuição normal padrão, da seguinte maneira:
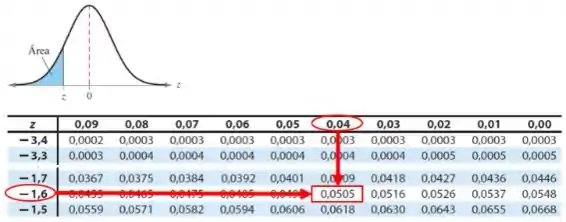
Como esse teste é unilateral à esquerda, a área correspondente para é:
Passo 3
Por fim iremos tomar a decisão de rejeitar ou não rejeitar a hipótese nula ():
- Se 🡪 rejeita .
- Se 🡪 não rejeita .
Como o valor é maior que (), então não rejeita .
Eai, curtiram a resolução? Então te espero em mais exercícios!
Resposta
Não rejeita . Não há evidência suficiente, ao nível de significância de 1%, para rejeitar a afirmação.