Utilize a versão de amostras grandes do teste de Wilcoxon ao nível 0,05 de significância sobre os dados do Exercício 37 na Seção para decidir se a diferença da média verdadeira entre as concentrações externas e internas excedem 0,20 .
Passo 1
E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:

Utilize a versão de amostras grandes do teste de Wilcoxon ao nível 0,05 de significância sobre os dados do Exercício 37 na Seção para decidir se a diferença da média verdadeira entre as concentrações externas e internas excedem 0,20 .
vs. , em que , e porque , podemos usar o teste de amostra grande. A estatística de teste é , e rejeitamos se .
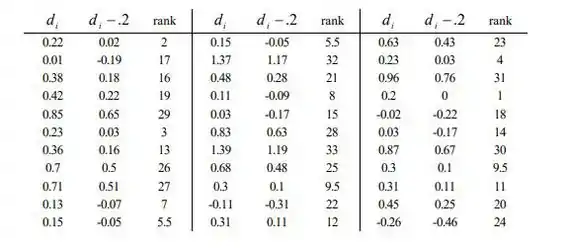
, então . Visto que , rejeitamos no nível significante .05.
Resposta
, então . Visto que , rejeitamos no nível significante .05.
Espero que tenham aprendido com essa questão, até a próxima !