Você deseja estimar, com 95% de confiança, a proporção populacional de adultos americanos que acham que deveriam estar poupando mais dinheiro. Sua estimativa deve ser precisa dentro de uma margem de erro de 5% da proporção populacional.
(a) Não há estimativas preliminares disponíveis. Encontre o tamanho mínimo da amostra necessário.
(b) Determine o tamanho mínimo da amostra necessário usando um estudo prévio que descobriu que 63% dos adultos americanos acham que deveriam estar poupando mais dinheiro. (Fonte: Pew Research Center.)
(c) Compare os resultados das partes (a) e (b).
Passo 1
Olá pessoal, vamos para mais um exercício?!
Como no item (a) diz que não tem uma estimativa preliminar de , usaremos e .
E pelo enunciado temos:
;
.
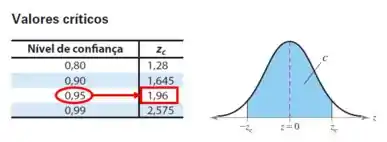
Temos que . Com isso conseguimos calcular o tamanho da amostra ():
Como é decimal, iremos arredondar para o próximo no inteiro, ou seja, .
Passo 2
Já no item (b) é dado a estimativa preliminar de 63%.
Logo:
E já temos e Encontrando o tamanho mínimo da amostra:
Como é decimal, iremos arredondar para o próximo no inteiro, ou seja, .
Resposta
(a) Sem estimativa preliminar, o tamanho mínimo da amostra deve ser pelo menos de 385 adultos americanos.
(b) Com uma estimativa preliminar de , o tamanho mínimo da amostra deve ser pelo menos de 359 adultos americanos.
(c) Precisamos de um tamanho de amostra maior quando não há estimativa preliminar disponível.