Escreva, de forma iterativa e recursiva, a função de Fibonacci que é definida da seguinte forma:
Fib(0) = 1
Fib(1) = 1
Fib(n) = Fib(n-1) + Fib(n-2) , para n >= 2
Em seguida, escreva um programa que apresente o resultado da execução das duas funções na tela e verifique, comparativamente, os tempos de cálculo de ambas as funções para Fib(35) e Fib(40).
Passo 1
Fala aí! Essa aqui vai dar um trabalhinho, mas vai valer a pena pra praticarmos a implementação de alguns conceitos. Se liga, vamos começar com a definição da função de Fibonacci de forma recursiva:
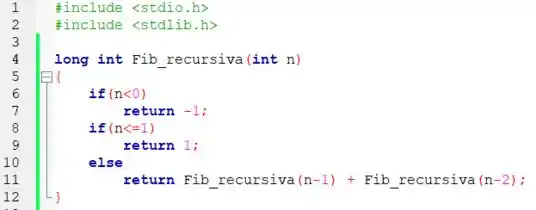
Bom, primeiro detalhe importante: declaramos a função do tipo long int pois, como os valores crescem muito rápido dependendo do parâmetro n passado, pode ser que o resultado não caiba em um simples int.
Dito isso, nossa função recursiva vai ficar bem simples, repare que aproveitamos as informações fornecidas pelo enunciado. Quando for fornecido um parâmetro n menor que zero, retornamos -1 para indicar que isso é inválido. Quando n estiver entre 0 e 1, retornamos 1 tal como o enunciado nos instruiu a fazer. Por fim, para qualquer outro valor de n, implementamos a expressão recursiva fornecida pelo próprio enunciado e retornamos o resultado.
Passo 2
Agora, vamos definir a mesma função de forma iterativa. Olha só como vai ficar:
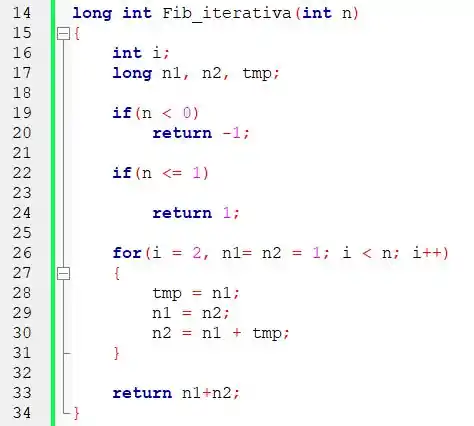
Repare que começamos da mesma forma, analisando os casos em que n é menor que zero e quando ele está entre 0 e 1. A diferença ocorre para os demais valores de n, pois agora que não podemos mais invocar a função de maneira recursiva, temos que recorrer a outro método.
O caminho escolhido então é o seguinte: definimos a variável int i, que representará cada iteração de 2 até n (lembre-se que já cobrimos os casos menores que 2) e outras três variáveis do tipo long int n1, n2 e tmp, que irão armazenar os números da sequência de Fibonacci. Aquelas instruções dentro do for podem parecer meio confusas, então deixa eu mostrar o que aconteceria na prática, vamos olhar para a sequência de Fibonacci que conhecemos e ver o que acontece com aquelas instruções. Na primeira iteração, quando i = 2, temos isso n1 = n2 = 1:
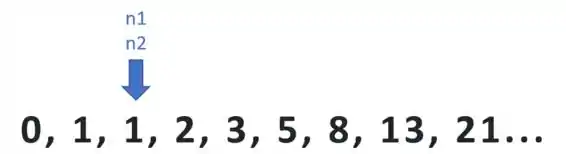
Ignoramos os dois primeiros valores (0 e 1) porque eles são tratados quando n = 0 ou n = 1 no if anterior. Depois disso, passamos o valor de n1 para tmp, o de n2 para n1 e somamos n1 e tmp para obter n2. Ficamos com:
Assim chegamos no próximo valor da sequência. Na próxima iteração, em i = 3, teremos:

Seguindo as instruções novamente, ficamos assim:
E assim seguimos até chegarmos em i = n. Espero que tenha ficado claro 😊
Passo 3
Pra finalizar a questão, vamos escrever lá no main um programa capaz de aplicar essas funções. Olha só como vai ficar:

Bem simples, né? Temos que simplesmente pedir um valor inteiro ao usuário e invocar uma função de cada vez passando esse valor como parâmetro.
Resposta
