Torres de Hanói. Todo cientista da computação iniciante precisa lutar contra certos problemas clássicos, e as Torres de Hanói (ver Figura 5.19) é um dos problemas mais famosos. A lenda diz que, em um templo no Extremo Oriente, sacerdotes estão tentando mover uma pilha de discos de um pino para outro. A pilha inicial tinha 64 discos dispostos em um pino e arrumados de baixo para cima por tamanho decrescente. Os sacerdotes estão tentando mover a pilha desse pino para um segundo pino sob as restrições de que apenas um disco é movido de cada vez, e em momento algum um disco maior pode ser colocado sobre um disco menor. Um terceiro pino está disponível para apoiar os discos temporariamente. Supostamente, o mundo terminará quando os sacerdotes completarem sua tarefa, de modo que não temos muito incentivo para facilitar seus esforços.
Vamos supor que os sacerdotes estejam tentando mover os discos do pino 1 ao pino 3. Queremos desenvolver um algoritmo que imprimirá a sequência exata de transferências de pino, disco a disco.
Se tivéssemos que resolver esse problema com a ajuda de métodos convencionais, ficaríamos presos na administração dos discos rapidamente. Em vez disso, se atacarmos o problema com a recursão em mente, ele imediatamente se tornará mais resolúvel. Mover n discos pode ser visto em termos de mover apenas n – 1 discos (e daí a recursão) da seguinte forma:
a) Mova n – 1 discos do pino 1 para o pino 2, usando o pino 3 como área de manutenção temporária.
b) Mova o último disco (o maior) do pino 1 para o pino 3.
c) Mova os n – 1 discos do pino 2 para o pino 3, usando o pino 1 como área de manutenção temporária.
O processo termina quando a última tarefa envolver mover n = 1 disco, ou seja, o caso básico. Isso é feito movendo o disco de modo trivial, sem a necessidade de uma área de manutenção temporária.
Escreva um programa que resolva o problema das Torres de Hanói. Use uma função recursiva com quatro parâmetros:
a) O número de discos a serem movidos.
b) O pino no qual esses discos estão empilhados inicialmente.
c) O pino para o qual a pilha de discos deve ser movida
d) O pino a ser usado como área de manutenção temporária.
Seu programa deverá imprimir as instruções exatas que ele usará para mover os discos do pino inicial para o pino de destino. Por exemplo, para mover uma pilha de três discos do pino 1 ao pino 3, seu programa deverá imprimir a seguinte série de movimentos:
1 → 3 (Isso significa mover um disco do pino 1 ao pino 3.)
1 → 2
3 → 2
1 → 3
2 → 1
2 → 3
1 → 3
Passo 1
Fala Galera!! Mais um exercício para treinar e ficar craque em programação. Bora lá!!!
O enunciado passa para nós todas as informações sobre a torre de Harói, e também nos diz que teremos que usar recursividade no nosso programa.
Para facilitar nossa vida, bora pensar em uma função que faça todo processo para mover os discos e chamar ela dentro do nosso programa e pedir para que o usuário digite o numero de disco que a torre irá ter. O numero de haste será fixo, ou seja, só teremos 3 hastes na torre.
Passo 2
Vamos construir a lógica da nossa função. Primeiro, chamamos as três hastes origem, auxiliar e destino de start, tempo e end, respectivamente. Para resolver o problema, cedo ou tarde o disco inferior (= o primeiro de baixo pra cima) deverá ser movido de start para end. Nesse ponto, todos os discos restantes estarão empilhados em forma decrescente na haste auxiliar temp. Após mover o disco inferior de start para end, os discos restantes terão que ser movidos de temp para end. Portanto, para um número n de discos, o problema será resolvido se seguirmos esses passos:
1) Mova os n-1 discos do topo de start para temp, usando end como auxiliar.
2) Mova o disco de baixo de start para end.
3) Mova os n-1 discos de tempo para end, usando start como auxiliar.
Passo 3
Agora vamos escrever nossa função em C. Ela ficará da seguinte forma:
/* torre imprime recursivamente instruções para discos em movimento da haste start à haste end usando haste temp para armazenamento temporário */
void tower( int c, int start, int end, int temp ){
/* cenário base */
if ( c == 1 ) {
printf( "%d --> %d\n", start, end );
return;
}/* fim do if */
/* movimento c - 1 discos desde o início até a temp */
tower( c - 1, start, temp, end );
/* mover o último disco do início ao fim */
printf( "%d --> %d\n", start, end );
/* movimento c - 1 discos da temp. ao fim */
tower( c - 1, temp, end, start );
} /* fim da função */
Passo 4
Finalizamos nossa função, agora falta chamar ela dentro do nosso programa, ou seja, do main() e pedir para o usuário inserir o numero de disco para a torre. Ficando da seguinte forma:
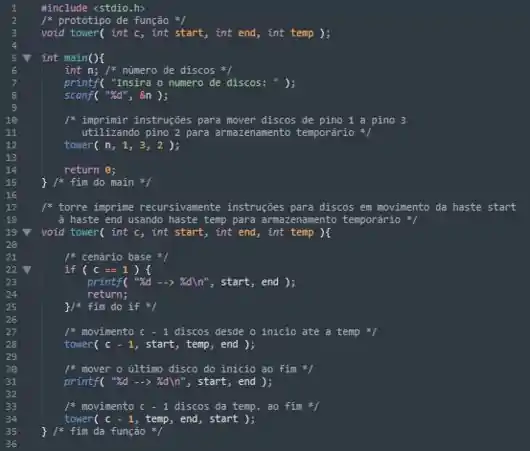
#include
/* protótipo de função */
void tower( int c, int start, int end, int temp );
int main(){
int n; /* número de discos */
printf( "Insira o numero de discos: " );
scanf( "%d", &n );
/* imprimir instruções para mover discos de pino 1 a pino 3 utilizando pino 2 para armazenamento temporário */
tower( n, 1, 3, 2 );
return 0;
} /* fim do main */
Agora juntamos tudo e nosso programa estará finalizado.
Por hoje é só Galeraa!! Até o próximo exercício.
Resposta
O programa final será: