Considere um sistema unidimensional fictício com um elétron. A função de onda para o elétron, representada a seguir, é ψ(x) = sen x de x = 0 para x = 2π.
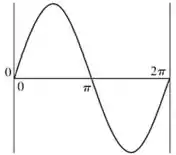
(a) Faça um esboço da densidade de probabilidade, ψ2(x), de x = 0 para x = 2π.
(b) Para que valor, ou valores, de x haverá maior probabilidade de encontrar o elétron?
(c) Qual é a probabilidade de que o elétron seja encontrado em x = π? Como esse ponto é chamado em uma função de onda? [Seção 6.5]
Passo 1
Gente, pode parecer complexo por envolver vários conceitos matemáticos no meio, mas é só visualização mesmo.
No caso, a Função de Onda do Elétron, ou Equação de Schrödinger , representa uma função periódica do elétron com característica probabilística de encontro de um elétron ao redor de um orbital.
A representação física da função de onda é condicionada ao seu quadrado, que representa a DENSIDADE PROBABILÍSTICA DE ENCONTRO DO ELÉTRON em uma determinada distância do núcleo.
Se uma onda possui amplitudes positivas e negativas, elevar sua equação ao quadrado não muda suas características, mas ELIMINA REGIÕES NEGATIVAS.
Ex.:
Sendo ψ(x) é uma função de onda como:
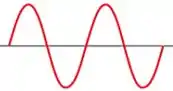
Então, ψ2(x) será:
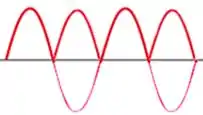
Onde teremos as seguintes informações:
1º) Os pontos de MAIOR AMPLITUDE serão os pontos no espaço com MAIOR DENSIDADE DE PROBABILIDADE DE ENCONTRO DA PARTÍCULA;
2º) As intersecções com o eixo horizontal serão chamadas de NÓS ou REGIÕES NODAIS e representam probabilidade NULA de encontro de elétrons;
Passo 2
Sendo assim, é possível escrever as considerações dos exercícios de acordo com a teoria nos seguintes sentidos:
(a)
O esboço do gráfico representado pela função
→ ψ(x) = sen x de x = 0 para x = 2π
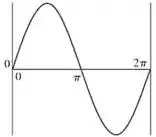
seria dado por:
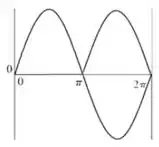
→ ψ2(x) = sen2(x) de x = 0 para x = 2π
(b)
Os pontos com maior probabilidade de encontrar elétrons serão concedidos através dos intervalos de maior amplitude no gráfico da função de onda.
Estando a equação da questão matematicamente coerente, os pontos do intervalo serão fornecidos de acordo com:
ψ(x) = sen x → -1 ≤ sen x ≤ 1
ψ2(x) = sen2(x) → 0 ≤ sen2x ≤ 1
Sendo que:
sen2x = 1 quando x = π/2 + kπ, k ∈ 𝜡
(c)
O elétron dessa função de onda NUNCA poderá ser encontrado em x = π, visto que sua probabilidade também será exercida de acordo com a equação
ψ2(x) = sen2(x) → 0 ≤ sen2x ≤ 1
Onde:
sen2x = 0 quando x = 0 + kπ, k ∈ 𝜡
Isso se dá pois, assim como 0 e 2π, por exemplo, π é um ponto de intersecção com o eixo horizontal e, na função de onda, é chamado Nó ou Região Nodal representando regiões do espaço cujas probabilidades de encontro do elétron são zero.
Resposta
(a) Faça um esboço da densidade de probabilidade, ψ2(x), de x = 0 para x = 2π.
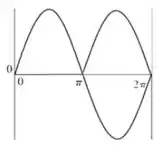
(b) x = π/2 + kπ, k ∈ 𝜡.
(c) Nenhuma, pois π é um ponto de Nó / Região Nodal.