Enunciado
Química - Russel, Quimica Geral - Vol 2- Ed: 1º - Capítulo 13.Problemas - Ex. 1
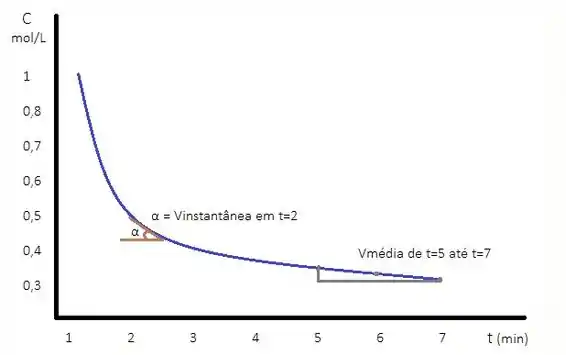
Esboce um gráfico mostrando como pode diminuir a concentração de um reagente com o tempo. Recorrendo ao seu gráfico, explique a diferença entre as velocidades média e instantânea.
Passo 1
Inicialmente, como o enunciado não especifica nada sobre a reação em questão, entenderemos que o gráfico pedido é o mais genérico possível. Assim, sabendo que a concentração dos reagentes vai diminuir com o passar do tempo, um gráfico possível seria:
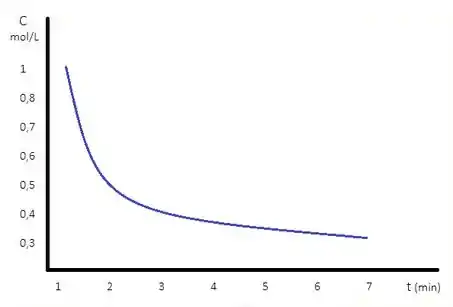
No gráfico acima, colocando o eixo y como a concentração do reagente e o eixo x como o tempo, podemos representar a diminuição da concentração do reagente conforme passa o tempo da reação. Isso ocorre, pois, toda reação química os reagentes serão consumidos e os produtos serão formados. Nesse caso em específico, não estamos preocupados com a equação desse gráfico, visto que para determiná-la precisaríamos de mais informações a respeito da reação química representada pelo gráfico.
Passo 2
Feito o esboço do gráfico de forma genérica, vamos utilizá-lo para explicar a diferença entre as velocidades médias e instantâneas.
A velocidade de consumo média dos reagentes sempre será dada pela diferença das concentrações sobre o tempo decorrido.
Uma forma fácil de ver isso é fazer a analogia com a física. Lembra da velocidade média lá da física? Que é igual a variação do espaço pelo tempo?
Então, na química, como velocidade usada é a velocidade de consumo do reagente, temos que pensar que o nosso ∆S é na verdade ∆Concentração do reagente, assim, temos:
Isso fica evidenciado no gráfico quando pegamos 2 pontos distintos e calculamos sua velocidade média de consumo utilizando a fórmula acima.
Observação: Como o reagente está sendo consumido, a concentração final dele será menor que a inicial, o que gera um negativo. Assim, a velocidade de consumo do reagente A será negativa.
Passo 3
Beleza, mas e a velocidade de consumo instantânea?
A velocidade de consumo instantânea dos reagentes ela será dada pelo coeficiente angular (inclinação) da reta tangente ao gráfico C x t, no tempo em que estivermos analisando (por isso o ‘‘instantânea’’). Ou seja, a velocidade de consumo instantânea é igual ao limite da variação de concentração para uma variação de tempo muitoooo pequena (infinitesimal).
Novamente, podemos fazer uma analogia com a física. Lá, estudamos que velocidade instantânea é o limite da velocidade escalar média, quando o intervalo de tempo tende a zero, ou seja:
Assim, na química, como a velocidade é a de consumo dos reagentes, faz sentido utilizarmos variação da concentração ao invés de ∆S.
Além disso, esse limite que aparece nas velocidades instantâneas tem um nome na matemática, é a definição de derivada. Ou seja, podemos resgatar todos aqueles conceitos de derivada que temos da matemática aqui para a química. Um deles é que a derivada da função em um ponto será numericamente igual ao coeficiente angular da reta tangente ao gráfico naquele mesmo ponto. Isso pode ser útil em outras questões envolvendo gráficos.
Resposta
Finalmente, entendendo como que funciona a velocidade de consumo média e a velocidade de consumo instantânea, podemos representar as duas no gráfico e deixá-lo ainda mais completo:
