A fonte de tensão no circuito da Figura P17.33 está gerando o sinal
a) Calcule .
b) Calcule .
c) Calcule .
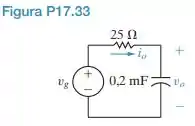
Passo 1
Falaaa, pessoal! Como vocês estão?
Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre transformada de Fourier!
- Desenvolvendo o sistema acima, podemos o expressar como:
- Como temos:
- Na fase dominante, temos que:
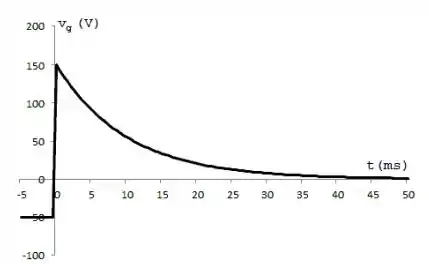
Portanto, temos que, no momento t=0:
No momento t=0+, temos que o circuito vai ser:
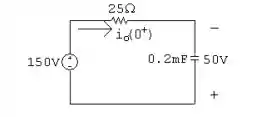
Ou seja:
Passo 2
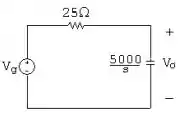
Podemos ver então que:
Com isso, temos:
Portanto:
Logo:
Colocando em termos de K, temos:
Portanto, temos:
Resposta
- Item a:
- Item b:
- Item c: