As funções de onda que correspondem a estados de energia diferente da partícula em uma caixa são mutuamente “ortogonais”, pois, se as duas funções de onda são multiplicadas, uma pela outra, e, então, integradas sobre a dimensão da caixa, o resultado é zero. (a) Confirme que as funções de onda de n =1 e n=2 são ortogonais. (b) Demonstre, sem fazer cálculos, que todas as funções de onda com n ímpar são ortogonais a todas as funções com n par.
Passo 1
E ai galera, beleza?
Seguinte, essa questão pede no item (a) para confirmar que duas funções de onda de n=1 e n=2 são mutuamente ortogonais, ou seja, se as duas funções de onda são multiplicadas, uma pela outra, e, então, integradas sobre a dimensão da caixa, o resultado é zero.
Em resumo, seria isso aqui:
No caso, função de onda é dada por:
Para n=1 e n=2, temos:
Tranquilo?? Agora é só a gente verificar se elas são ortogonais, então, temos:
Vamos deixar de lado os termos porque eles são constantes, beleza? E para facilitar vamos usar o Wolfram Alpha para resolver as integrais, afinal, não estamos aqui pra estudar cálculo hoje né? hahaha
Assim:
Logo, verificamos que as funções são ortogonais!

Passo 2
Agora, no item (b) pede para demonstrar, sem fazer cálculos, que todas as funções de onda com n ímpar são ortogonais a todas as funções com n par.
Galera, seguinte, o que temos, para um caso geral é isso aqui:
Já que (2n) sempre representa um número par qualquer e (2k-1) sempre representa um número ímpar qualquer para todo n e para todo k.
Show! Vamos usar a sugestão da questão e plotar o gráfico da seguinte função:
Com a ajuda do Geogebra, fazendo n=1, k=1 e L=5, temos:
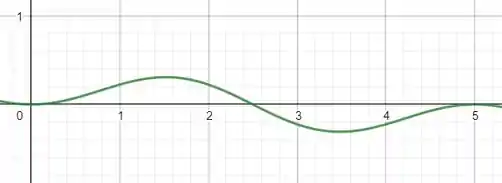
Note que, as áreas da parte de cima do gráfico e da parte de baixo são iguais! Mas o que isso significa?? Isso quer dizer que o resultado daquela integral feia que escrevemos lá em cima é zero! Sem fazer nenhuma conta!
Se você quiser brincar no Geogebra e alterar os valores para n, k e L, verá que isso sempre ocorre. Assim, demonstramos, sem fazer cálculos, que todas as funções de onda com n ímpar são ortogonais a todas as funções com n par. A matemática é linda, né? 
Passo 3
Olha, a questão já acabou por aqui, mas caso você seja um aluno curioso e queira fazer o item (b) fazendo cálculos, vou te mostrar aqui nesse passo.

Mas lembra que a questão não pede isso, então se quiser já pode pular pra próxima sem crise, beleza??
Então vamo lá!
Galera, lembra da integral do passo 2
Então, se a gente resolver ela e encontrar que o resultado disso é zero, demonstramos o que a questão pede. De novo, pra resolver essa integral aqui a gente pode usar o Wolfram e desconsiderar o termo constante pra facilitar!
Contando com a ajuda do nosso software amiguinho, temos:
=0
Logo, todas as funções de onda com n ímpar são ortogonais a todas as funções com n par.
Fechooou!! Vamos pra próxima?? :D

Resposta
- Analisando a área sobre o gráfico verificamos que sempre são ortogonais,