Enunciado

Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 25.Questões e Problemas - Ex. 24fghij

Problema Desafiador: Horlick descreveu os princípios matemáticos da transformada de Fourier, interpretou-os graficamente e descreveu como podem ser empregados em espectroscopia analítica.11 Leia o artigo e responda às seguintes questões:

(a) Defina o que é domínio do tempo e domínio da freqüência

(b) Escreva as equações para a integral de Fourier, para sua transformação e defina cada um dos termos das equações.

(c) O artigo mostra os sinais para o domímio do tempo para uma onda co-senoidal de 32 ciclos, uma onda co-senoidal de 21 ciclos, bem como as transformadas de Fourier desses sinais. Como se altera a forma do sinal no domínio das freqüências quando o número de ciclos das ondas originais se modifica?

(d) O autor descreve o fenômeno de atenuação (damping). Que efeito a atenuação exerce sobre as ondas co-senoidais originais? Que efeito isso acarreta no resultado da transformada de Fourier?

(e) O que é uma função de resolução?

(f) O que é o processo de convolução?

(g) Discuta como a escolha da função de resolução pode afetar a aparência do espectro.

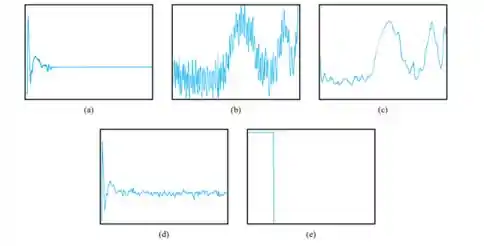
(h) A convolução pode ser empregada para diminuir a quantidade de ruído no espectro. Considere os gráficos abaixo de sinais no domínio do tempo e no domínio da freqüência. Identifique os eixos para os cinco gráficos. Por exemplo, o gráfico (b) deve ser rotulado com amplitude versus tempo. Caracterize cada gráfico como pertencendo ao domínio do tempo ou da freqüência.

(i) Descreva as relações matemáticas entre os gráficos. Por exemplo, como se pode chegar ao gráfico (a) a partir dos gráficos (d) e (e)?

(j) Discuta a importância prática de se poder reduzir o ruído nos sinais espectroscópicos

Passo 1

Falaiii meus amores, cêis tão suave?

“Se alguma coisa está dificil de ser feita, é porque não é para ser feita" # sóquenão”

(f) O processo de convolução é, em termos simples, tornar uma média de execução. É usado para descrever os efeitos de qualquer instrumento em particular sobre um fato observador. Em termos matemáticos, é uma função derivada de duas funções dadas por integração que expressa como uma adapta a forma da outra.

Passo 2

(g) O espectro observador é afetado pelo fator de resolução de três maneiras diferentes. Se a função de resolução for mais larga que a linha medida, então a largura e a forma da linha observada são as da função de resolução. Se a função de resolução for relativamente igual à linha medida, a linha observada será uma combinação das duas. Se a função de resolução for mais estreita do que a linha medida, então a largura e forma da linha observada é a linha medida.

Passo 3

(h) Rotularemos e caracterizaremos cada parcela apresentada no texto

(a) amplitude versus frequência – sinal no domínio da frequência

(b) amplitude versus tempo – sinal no domínio do tempo

(d) amplitude versus frequência – sinal no domínio da frequência

(e) amplitude versus tempo – sinal no domínio do tempo

Passo 4

(I) Existe uma dependência inversa da largura da função no domínio da frequência e do comprimento da função no domínio do tempo. Por causa dessa dependência, gráficos do domínio da frequência podem ser usados matematicamente para determinar o domínio do tempo e vice-versa.

Os gráficos de determinado ciclo de onda podem ser usados matematicamente para determinar o mesmo gráfico. Isso pode ser feito com funções no domínio da frequência e no domínio do tempo.

Passo 5

(J) O ruido é causado por variações dentro da instrumentação e, em última análise, reduz a sensibilidade desse instrumento. Ao reduzir o ruído, há menos variáveis para lidar e a sensibilidade geral aumenta.

Certo, cérebro, eu não gosto de você e nem você de mim, então faça tudo certo pelo menos uma vez para que eu possa continuar te matando com estudos, certo?

Resposta

Resposta nos passos.