Problema Desafiador: Horlick descreveu os princípios matemáticos da transformada de Fourier, interpretou-os graficamente e descreveu como podem ser empregados em espectroscopia analítica.11 Leia o artigo e responda às seguintes questões:
(a) Defina o que é domínio do tempo e domínio da freqüência
(b) Escreva as equações para a integral de Fourier, para sua transformação e defina cada um dos termos das equações.
(c) O artigo mostra os sinais para o domímio do tempo para uma onda co-senoidal de 32 ciclos, uma onda co-senoidal de 21 ciclos, bem como as transformadas de Fourier desses sinais. Como se altera a forma do sinal no domínio das freqüências quando o número de ciclos das ondas originais se modifica?
(d) O autor descreve o fenômeno de atenuação (damping). Que efeito a atenuação exerce sobre as ondas co-senoidais originais? Que efeito isso acarreta no resultado da transformada de Fourier?
(e) O que é uma função de resolução?
(f) O que é o processo de convolução?
(g) Discuta como a escolha da função de resolução pode afetar a aparência do espectro.
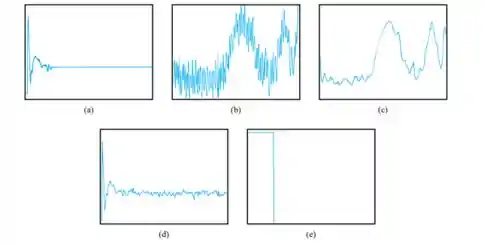
(h) A convolução pode ser empregada para diminuir a quantidade de ruído no espectro. Considere os gráficos abaixo de sinais no domínio do tempo e no domínio da freqüência. Identifique os eixos para os cinco gráficos. Por exemplo, o gráfico (b) deve ser rotulado com amplitude versus tempo. Caracterize cada gráfico como pertencendo ao domínio do tempo ou da freqüência.
(i) Descreva as relações matemáticas entre os gráficos. Por exemplo, como se pode chegar ao gráfico (a) a partir dos gráficos (d) e (e)?
(j) Discuta a importância prática de se poder reduzir o ruído nos sinais espectroscópicos
Passo 1
Falaaaa moçadinha, show de bola?
Como diz o Homem de ferro “Eu tenho um plano. Ataque!”

Bora atacar esse problemaaaaaaa junto comigoo.
- O domínio do tempo é a análise de funções matemáticas em relação ao tempo. O domínio da frequência é a análise de funções matemáticas em relação á frequência.
- As seguintes equações são a integral de Fourier
- Quanto maior o número de ciclos, mais estreito se torna o sinal do domínio da frequência.
- Quando uma onda cosseno sofre amortecimento, a forma da ilha é reduzida, tornando-se menos gaussiana e mais parecida com uma linha, dependendo do amortecimento da onda. Isso afetará as transformações de Fourier adicionando outro fator exponencial à equação.
- A função determina a forma imposta em uma linha espectral. Pode assumir duas formas limitantes: para limitada por difração, assume a forma de função e para limitada por largura de fenda, pode assumir a forma de uma função triangular.
Passo 2
Onde é a frequência, x é o comprimento ou tempo é i é 1;
A equação a seguir é a transformação de Fourier.
Onde é a frequência e o x e o comprimento ou tempo.
Passo 3
Quanto menor o número de ciclos, mais amplo se torna o sinal do domínio da frequência.
Passo 4
Passo 5
“Às vezes é preciso aprender a correr antes de começar a andar”

Resposta
Resposta nos passos.