Repita o Problema 17.26, mas substitua por .
Passo 1
Falaaa, pessoal! Como vocês estão?
Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre transformada de Fourier!
- Da solução do problema anterior temos que:
- Diante dos conhecimentos adquiridos acima, temos que:
- Diante dos conhecimentos adquiridos acima, temos que:
- Novamente, pelo que obtivemos anteriormente chegamos no seguinte esquema:
- Pelo que sabemos acima, temos que a resposta é sim.
Com isso:
Temos então:
Logo:
Portanto:
Passo 2
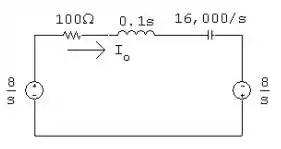
Ou seja:
Por fim:
Resposta
- Item a:
- Item b:
- Item c:
- Item d:
- Item e: Sim.