Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 1.J - Ex. 12

C 6 H 5 N H 3 C l é um sal cloreto com um cátion ácido. (a) Se 50,0 g de C 6 H 5 N H 3 C l são dissolvidos em água para preparar 150   m l de uma soluão, qual é a molaridade inicial do cátion? (b) Escreva a equação química da reação de transferência de próton do cátion para a água. Identifique o ácido e a base nessa reação.

Passo 1

Letra (a)

Para calcular a molaridade do cátion precisamos primeiro saber a molaridade do composto, para isso é necessário calcular a sua massa molar massa molar.

Dados dos elementos:

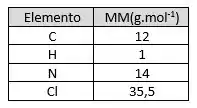
Massa molar ( M M ) do C 6 H 5 N H 3 C l :

M M =   6 × 12 + 8 × 1 + 14 + 35,5 = 129,5   g . m o l - 1

Temos que a concentração é a razão entre o número de mols com o volume.

C = n V

n = 50 g 129,5 g . m o l - 1 ≅ 0,386   m o l

C = 0,368   m o l 0,150   L ≅ 2,574   m o l . L - 1

Como a relação do cátion para o composto é de 1 para 1, a concentração do cátion será a mesma do composto.

C = 2,574   m o l . L - 1

Passo 2

Para o sal C 6 H 5 N H 3 C l , temos que o cátion é o C 6 H 5 N H 3 + e o ánion é o C l - . Sendo assim a equação química da reação de transferência de próton do cátion para a água é:

C 6 H 5 N H 3 + a q + H 2 O l → C 6 H 5 N H 2 a q + H 3 O + ( l )

Passo 3

Segundo Bronsted-Lowry, um ácido é um doador de prótons e uma base é um aceitador de prótons. Portanto em solução, o ácido doará um próton ( H + ) enquanto a base receberá esse próton.

Na reação acima o C 6 H 5 N H 3 + doa um próton para a água, logo, o C 6 H 5 N H 3 + a q é o ácido e a água é a base.

Resposta

(a)

C = 2,574   m o l . L - 1

(b)

C 6 H 5 N H 3 + a q + H 2 O l → C 6 H 5 N H 2 a q + H 3 O + ( l )

Ácido: C 6 H 5 N H 3 +

Base:   H 2 O

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

E.26 O sulfato de cobre ( Ι Ι ) anidrido é difícil de obter completamente seco. Que massa de sulfato de cobre ( Ι Ι ) restaria após a remoção de toda a água de 250 g de CuSO4 . 5H2O?.
E.33 A queda dos dentes pode ser retardada com o uso de pasta de dentes fluorada. O íon fluoreto converte a hidroxiapatita, C a 5 P O 4 3 O H do esmalte do dente em fluorapatita, qual seria a percenta
E.23 (a) Calcule a massa, em gramas, de uma molécula de água. (b) Determine o número de moléculas de H20 em 1,00 Kg do composto.
E.30 O isótopo silício-28 foi proposto como um novo padrão para as massas molares dos elementos, porque ele pode ser preparado em elevado grau de pureza. A massa de um átomo de silício-28 é 4,64567 ×
E.25 Um químico mediu 8,61 g de cloreto de cobre ( Ι Ι ) tetra-hidratado, CuCl2 . 4H2O. (a) Quantos mols de CuCl2 . 4H2O foram medidos? (b) Quantos mols de íons Cl- estão presentes na amostra? (c) Qua