Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Ciclo de Brayton

Ver Todos os Exercícios

Teoria

Bora aprender sobre o Ciclo de Brayton com o RespondeAí!?

O Ciclo de Brayton é um ciclo termodinâmico, utilizado nas turbinas de gás, que descreve o funcionamento de um motor térmico!

Mas qual é a diferença entre o Ciclo de Brayton e o Ciclo de Rankine?

Enquanto o ciclo de Rankine é considerado o ideal para operações com vapor e trocas de fase. Já o ciclo de Brayton é o ideal para quando não há troca de fases, ou seja, o fluido está sempre no estado de vapor. Além disso, enquanto o ciclo de Rankine utiliza água como fluido de trabalho o fluido de trabalho do ciclo Brayton é o ar.

O ciclo de Brayton é utilizado nas turbinas a gás e é formado pelos mesmo processos do que o ciclo de Rankine, que são duas isentrópicas e duas isobáricas. Vamos ver como ficam o diagrama para este ciclo, podendo o ciclo ser aberto ou fechado.

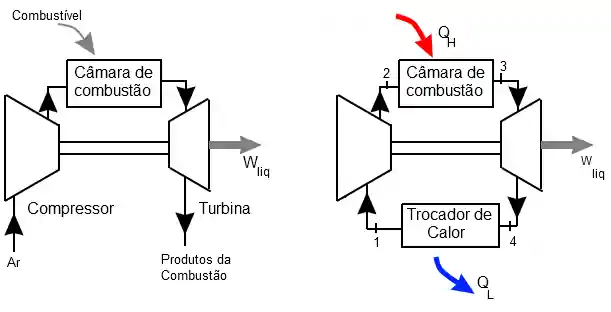
Representação do ciclo de Brayton.
Representação do ciclo de Brayton.

À esquerda temos a representação do ciclo de Brayton aberto, a qual há um fluxo constante de entrada de ar e saída dos gases da combustão. Já na direita temos o ciclo fechado, trabalhando sempre com a mesma massa que fica recirculando. Um exemplo de uso do ciclo fechado é nos reatores nucleares!

Etapas do Ciclo de Brayton

O seu funcionamento é muito parecido com os outros ciclos termodinâmicos, uma diferença que pode ser observada é que ao invés da bomba (que transporta líquidos) temos um compressor (que transporta gases).

O compressor eleva a pressão na câmara de combustão, aumentando a quantidade de ar e, portanto, o trabalho líquido. Vamos ver os processos envolvidos e suas representações nos diagramas e :

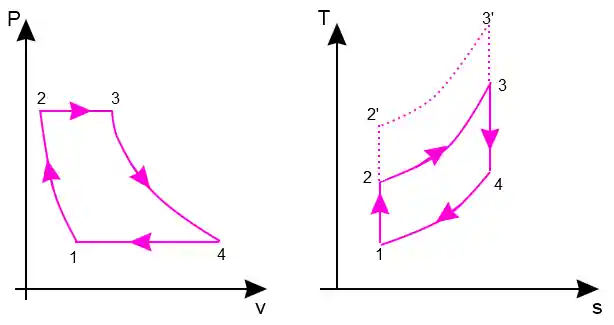
Diagramas: P X v e T X s para o Ciclo de Brayton.
Diagramas: P X v e T X s para o Ciclo de Brayton.
  • 1 – 2 (Compressor): O ar é comprimido isentropicamente, o que requer entrada de trabalho .
  • 2 – 3 (Câmara de combustão): Processo isobárico no qual há injeção de combustível que leva a combustão e gera calor . No caso do ciclo fechado a combustão é externa e só a entrada de calor .
  • 3 – 4 (Turbina): Os gases aquecidos se expandem isentropicamente realizando trabalho .
  • 4 – 1 (Trocador de calor): No caso de ciclo fechado, calor, , é retirado do sistema isobaricamente . Já para o sistema aberto os produtos são eliminados na atmosfera (que maldade) e ar fresquinho entra no sistema.

Observando o diagrama vemos que que as curvas 2 – 3 e 4 – 1 são isobáricas ao aumentarmos a pressão geramos mais trabalho, e consequentemente mais potência, como podemos observar pelas curvas 2’ – 3’ . Agora vamos ver o porquê!

Eficiência

Vamos calcular a eficiência de um ciclo de Brayton então! Vamos lembrar que a eficiência de uma máquina térmica se calcula como:

Como, pela primeira lei da termodinâmica temos que:

Então:

Agora presta atenção! Os dois processos que envolvem  e  são processos isobáricos, logo, a quantidade de calor transferida pode ser calculada como o calor específico a pressão constante  vezes a diferença de temperatura .

Assim, a eficiência é dada por:

Colocando o   e  em evidência no numerador e denominador, respectivamente:

Uma particularidade do Processo Adiabático

Agora vamos falar sobre uma particularidade do processo adiabático e consequentemente do isentrópico, que será discutida mais profundamente no capítulo de relações de Maxwell. Por agora o importante é lembrar que, para processos isentrópicos a seguinte relação é válida:

A partir da Lei dos gases ideais:

Podemos escrever o volume específico como:

Assim:

Comparando dois pontos e temos:

Podemos cortar o :

E por fim, reorganizando os termos:

Aplicação para a eficiência do ciclo de Brayton

Agora vamos aplicar essa relação para o nosso ciclo. Primeira temos que lembrar que  e , então

Assim,:

e:

Olha só que se subtrairmos dos dois lados, vamos chegar em algo próximo à nossa eficiência

Como a eficiência é dada por:

Podemos, agora, simplificar para:

Mas como estamos falando de isobáricas é legal deixar isso em função da pressão, que agora é fácil basta usar a equação:

E a eficiência vai ficar da forma:

Agora conseguimos mostrar que a eficiência depende apenas das pressões em e e, é claro, de qual fluido estamos falando, isso por causa do  que varia de fluido para fluido.

O ciclo de turbina a gás com regeneração

Você também pode se deparar com o ciclo composto de regeneração. Um regenerador é um equipamento que utiliza o calor dos gases da turbina para aquecer o ar antes deste entrar na turbina. O ciclo para apenas um estágio fica muito parecido com o ciclo convencional, mas para múltiplos estágios, de compressores e turbinas, fica parecendo um serrote.

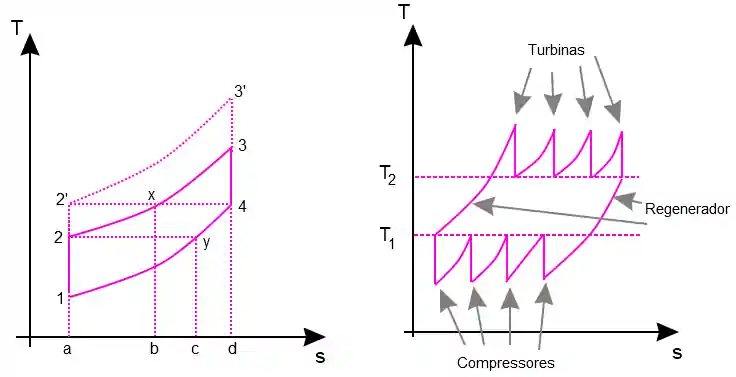
Ciclo da turbina a gás com regeneração.
Ciclo da turbina a gás com regeneração.

Na figura acima, podemos observar na esquerda o ciclo regenerativo com apenas um compressor e uma turbina, nele, o calor  entra no ciclo apenas no trecho , de o calor é o regenerado pela regenerador, isso faz com que  diminua aumentando a eficiência do ciclo. O mesmo ocorre, mas em sentido inverso no trecho . De o calor excedente da turbina aquece o trecho , por meio do regenerador. O  passa a ser apenas o trecho .

Podemos observar também, que:

  • As retas verticais acima de são os processos que ocorrem nas turbinas (Isentrópicas).
  • As retas verticais abaixo de são os processos que ocorrem nos compressores (Isentrópicas).
  • A curva entre e  são os processos que ocorre no regenerador (isobáricas).
  • As curvas acima de são os processos que ocorrem nas câmaras de combustão (isobáricas).
  • As curvas abaixo de são os processos que ocorrem nos resfriadores (isobáricas).

A eficiência deste ciclo é parecida com o ciclo de Brayton convencional mas depende também da temperatura e é dada, para o ciclo de um estágio, por:

Portanto, agora além de depender, também das temperaturas, a eficiência é inversamente proporcional a diferença de pressões!

Ainda está com dúvidas? Então dá uma olhadinha aqui nesse vídeo que temos sobre o ciclo de Brayton

Agora você já esta pronto pra praticar com exercícios!

Eficiência

Uma particularidade do Processo Adiabático

Aplicação para a eficiência do ciclo de Brayton

O ciclo de turbina a gás com regeneração

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

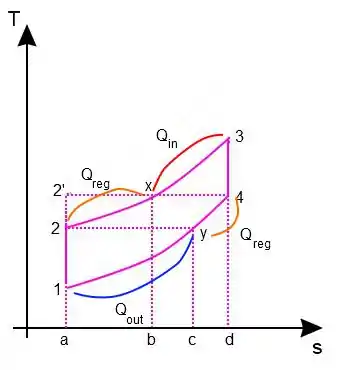
Qual a diferença que pode ser observada entre um ciclo Brayton padrão e um ciclo com regeneração em relação ao calor absorvido e rejeitado e em relação à eficiência? Desenhe um gráfico que mostre claramente onde o calor regenerado aparece.

Passo 1

Num ciclo regenerativo o calor excedente da turbina é utilizado para pré aquecer o gás que está prestes a entrar na câmara de combustão, com isso o calor permanece fluindo dentro do próprio sistema e não é mais considerado como q H . Isso ocorre de forma análoga para q L .

Passo 2

A eficiência de um ciclo regenerativo depende das pressões e temperaturas e, ao contrário do ciclo padrão, é inversamente proporcional a taxa de compressão.

η = 1 - T 1 T 3 p 2 p 1 k - 1 k

Passo 3

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #2

USP, Ciclo de motores a gás, Prof. Dr. Silvio de Oliveira Júnior, 2011, p. 19

Considere um ciclo ideal de Brayton operando com ar que entra no compressor a 100 kPa e 300 K, com uma vazão de 5 m³/s. a relação de pressões do compressor é 10. A temperatura de entrada na turbina é 1400 K. Determine: a) a eficiência térmica do ciclo; b) a relação entre o trabalho produzido pela turbina e consumido pelo compressor; c) a potência líquida gerada pelo ciclo em kW. Dado: γ a r = 1,4 ; c p = 1,004 k J k g ; R a r = 0,287 k J k g   K

Passo 1

Para calcular a eficiência basta utilizar a equação que vimos no conteúdo, já que a relação de pressões e o γ do ar foi dado

η = 1 - 1 p 2 p 1 γ - 1 γ

η = 1 - 1 10 1,4 - 1 1,4 = 48 %

Passo 2

Vamos calcular as temperaturas nas quais o ar sai do compressor e da turbina por meio da relação entre pressão e temperatura para processos isentrópicos.

T 2 T 1 = p 2 p 1 γ - 1 γ

Para o compressor

T 2 300 = 10 1,4 - 1 1,4

T 2 = 300 ⋅ 10 1,4 - 1 1,4 = 579 K

Como a taxa de compressão é igual para o compressor e para a turbina, temos

1400 T 4 = 10 1,4 - 1 1,4

T 4 = 1400 10 1,4 - 1 1,4 = 725 K

Passo 3

Agora vamos calcular o trabalho consumido pelo compressor. Sabemos que o trabalho numa isentrópica e igual a variação da entalpia Δ H , que por sua vez é igual a c p ⋅ Δ T , portanto

w c = c p ⋅ Δ T = 1,004 ⋅ 579 - 300 = 280 k J k g

w t = c p ⋅ Δ T = 1,004 ⋅ 1400 - 725 = 678 k J k g

Passo 4

A relação entre o trabalho produzido pela turbina e consumido pelo compressor

w t w c = 678 280 = 2,42

Passo 5

A potência líquida é igual a potência da turbina menos a potência do compressor

w l i q = w t - w c = 678 - 280 = 398 k J k g

Resposta

a) η = 48 %

b) w t w c = 2,42

c) w l i q = 398 k J k g

Exercício Resolvido #3

Elaboração própria

Demonstre que a eficiência de um ciclo de turbina a gás com uma etapa de regeneração ideal é igual a

η = 1 - T 1 T 3 p 2 p 1 k - 1 k

Considere 1 a entrada do compressor, 2 a entrada do regenerador, 3 a entrada da turbina e 4 o retorno ao regenerador.

Passo 1

O rendimento se calculo como

η = w l i q q H

Como q H é recebido no regenerador então temos que

q H = c p ( T 3 - T x )

e w t é o trabalho da turbina

w t = c p ( T 3 - T 4 )

e w c o trabalho do compressor

w c = c p ( T 2 - T 1 )

Assim

η = w t - w c q H = c p T 3 - T 4 - c p ( T 2 - T 1 ) c p ( T 3 - T x )

Passo 2

Como o regenerador é ideal T 4 = T x e q H = w t , logo

η = c p T 3 - T 4 - c p ( T 2 - T 1 ) c p ( T 3 - T 4 )

η = 1 - T 2 - T 1 T 3 - T 4

Aplicando T 1 e T 3 em evidência

η = 1 - T 1 ( T 2 T 1   - 1 ) T 3 ( 1 - T 4 T 3 )

Passo 3

Aplicar a relação de pressão e temperatura para processos isobáricos

p 3 p 4 = p 2 p 1 = T 2 T 1 γ γ - 1 = T 3 T 4 γ γ - 1

η = 1 - T 1 ( p 2 p 1 k - 1 k   - 1 ) T 3 ( 1 - p 1 p 2 k - 1 k )

η = 1 - T 1 T 3 p 2 p 1 k - 1 k

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #4

Escola politécnica da cidade de São Paulo, Lista de ciclo de motores a ar, p. 11

Considere um ciclo de turbina a gás ideal com dois estágios de compressão e dois estágios de expansão. A razão de pressão em cada estágio do compressor e da turbina é de 3. O ar entra em cada estágio do compressor a 300K e em cada estágio da turbina a 1200K. Considerando calores específicos constantes, determine a relação entre a potência necessária para acionar o compressor e a potência desenvolvida pela turbina, assim como o rendimento térmico do ciclo para o caso em que não há um regenerador. Dados: c p = 1,004 k J k g   k ; c v = 0,717 k J k g   K

Passo 1

Primeiro é interessante colocar esse problema num diagrama T   x   s para ser mais fácil de visualizar. Se lembra quando estamos trabalhando com mais de um estágio ele parece um serrote? Então vai ficar mais ou menos assim:

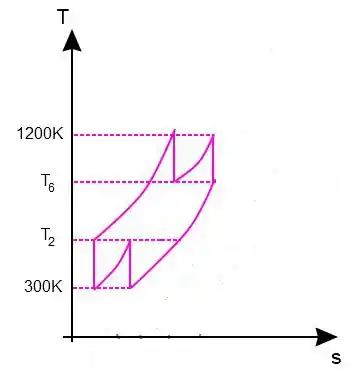
Passo 2

Como os processos nos compressores e nas turbinas são isentrópicos a relação entre pressão e temperatura é dada por

p 2 p 1 = T 2 T 1 γ γ - 1

Como nos foi dado a relação p 2 p 1 = 3 e um as temperaturas de entrada no compressor e na turbina, podemos achar a temperatura de saída de cada um.

Temos de lembrar, também que γ = c p c v

γ = 1,004 0,717 = 1,4

T 2 T 1 = p 2 p 1 γ - 1 γ

Calculando a temperatura de saída do compressor

T 2 300 = 3 1,4 - 1 1,4

T 2 = 300 ⋅ 3 1,4 - 1 1,4 = 411 K

Passo 3

Vamos fazer a mesma coisa para a saída da turbina

1200 T 6 = 3 1,4 - 1 1,4

T 6 = 1200 3 1,4 - 1 1,4 = 877 K

Passo 4

Os cálculos da potência e calor todos dependem da variação da entalpia. Para o compressor e a turbina, por ser uma isentrópica, a variação da entalpia é igual a c p ⋅ Δ T . O calor fornecido numa isobárica é dado, também, por c p ⋅ Δ T . Como são duas turbinas e dois compressores:

w c = 2 c p ⋅ Δ T 1 - 2

w t = 2 c p ⋅ Δ T 5 - 6

q H = c p ⋅ Δ T 4 - 5 + c p ⋅ Δ T ( 6 - 7 )

w c = 2 ⋅ 1,004 ⋅ 111 = 223 k J k g

w T = 2 ⋅ 1,004 ⋅ 323 = 649 k J k g

q H = 1,004 ⋅ 1200 - 411 + 1,004 ⋅ ( 1200 - 877 ) = 1116 k J k g

Passo 5

A relação entre a potência necessária para acionar o compressor e a potência desenvolvida pela turbina é:

w c w t = 223 649 = 0,34

Passo 6

O rendimento térmico do ciclo para o caso em que não há um regenerador

η = w t - w c q H = 649 - 223 1116 = 38 %

Resposta

A relação entre a potência necessária para acionar o compressor e a potência desenvolvida pela turbina é:

w c w t = 0,34

O rendimento térmico do ciclo para o caso em que não há um regenerador

η = 38 %

Exercício Resolvido #5

Escola politécnica da cidade de São Paulo, Lista de ciclo de motores a ar, p. 22

Considere um ciclo de turbina a gás ideal com dois estágios de compressão e dois estágios de expansão. A razão de pressão em cada estágio do compressor e da turbina é de 3. O ar entra em cada estágio do compressor a 300K e em cada estágio da turbina a 1200K. Considerando calores específicos constantes, determine a relação entre a potência necessária para acionar o compressor e a potência desenvolvida pela turbina, assim como o rendimento térmico do ciclo para o caso em que há um regenerador com eficiência de 75%. Dados: c p = 1,004 k J k g   k ; c v = 0,717 k J k g   K

Passo 1

Primeiro é interessante colocar esse problema num diagrama T   x   s para ser mais fácil de visualizar. Se lembra quando estamos trabalhando com mais de um estágio ele parece um serrote? Então vai ficar mais ou menos assim:

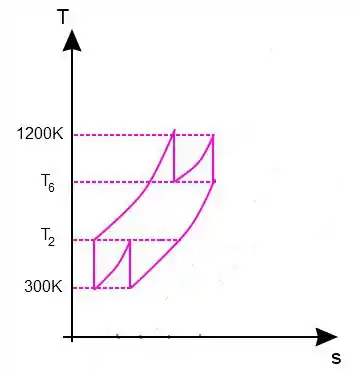
Agora, diferentemente do problema anterior o calor trocado entre T 6 e T 2 é o calor trocado no regenerador. Portanto, o cálculo do q H vai ser um pouquinho diferente.

Passo 2

Como os processos nos compressores e nas turbinas são isentrópicos a relação entre pressão e temperatura é dada por

p 2 p 1 = T 2 T 1 γ γ - 1

Como nos foi dado a relação p 2 p 1 = 3 e um as temperaturas de entrada no compressor e na turbina, podemos achar a temperatura de saída de cada um.

Temos de lembrar, também que γ = c p c v

γ = 1,004 0,717 = 1,4

T 2 T 1 = p 2 p 1 γ - 1 γ

Calculando a temperatura de saída do compressor

T 2 300 = 3 1,4 - 1 1,4

T 2 = 300 ⋅ 3 1,4 - 1 1,4 = 411 K

Passo 3

Vamos fazer a mesma coisa para a saída da turbina

1200 T 6 = 3 1,4 - 1 1,4

T 6 = 1200 3 1,4 - 1 1,4 = 877 K

Passo 4

Os cálculos da potência e calor todos dependem da variação da entalpia. Para o compressor e a turbina, por ser uma isentrópica, a variação da entalpia é igual a c p ⋅ Δ T . O calor fornecido numa isobárica é dado, também, por c p ⋅ Δ T . Como são duas turbinas e dois compressores:

w c = 2 c p ⋅ Δ T 1 - 2

w t = 2 c p ⋅ Δ T 5 - 6

q H = c p ⋅ Δ T 4 - 5 + c p ⋅ Δ T ( 6 - 7 )

Mas agora parte desse calor recebido pelo sistema é regenerado ou seja

q H = q H ( a n t i g o ) - q r e g e n e r a d o

E o calor regenerado é dado por

q r e g = η r e g ⋅ c p ⋅ Δ T 9 - 4

w c = 2 ⋅ 1,004 ⋅ 111 = 223 k J k g

w T = 2 ⋅ 1,004 ⋅ 323 = 649 k J k g

q H ( a n t i g o ) = 1,004 ⋅ 1200 - 411 + 1,004 ⋅ ( 1200 - 877 ) = 1116 k J k g

q r e g = 0,75 ⋅ 1,004 ⋅ 877 - 411 = 351 k J k g

q H = q H ( a n t i g o ) - q r e g e n e r a d o = 1116 - 351 = 765 k J k g  

Passo 5

O rendimento térmico do ciclo para o caso em que há um regenerador de 75% de eficiência é

η = w t - w c q H = 649 - 223 765 = 56 %

Resposta

O rendimento térmico do ciclo para o caso em que há um regenerador de 75% de eficiência é

η = 56 %

Exercício Resolvido #6

Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.265 – Exemplo 9.6

Ar entra no compressor, de um ciclo-padrão a ar Brayton (fechado), a 0,1 MPa e 15°C. A pressão na saída do compressor é de 1,0 MPa e a temperatura máxima no ciclo é 1100°C. Determine a pressão e atemperatura em cada ponto do ciclo, o trabalho no compressor, na turbina e o rendimento do ciclo. Dado: c p = 1,0035 k J k g   K

Passo 1

É sempre bom começar o exercício pelo estado o qual temos mais informações, nesse caso seria o ponto 1 (entrada no compressor) pois sabemos a pressão e a temperatura.

Sempre iremos utilizar a primeira e segunda lei que fornecem, respectivamente as equações:

w c = h 2 - h 1

s 2 = s 1

É necessário, também, lembrar da relação entre temperatura e pressão para isentrópicas:

T 2 T 1 = p 2 p 1 γ - 1 γ

Passo 2

Com isso podemos achar a temperatura do estado 2, lembrando que γ a r = 1,4

T 2 T 1 = p 2 p 1 γ - 1 γ

T 2 T 1 = 10 1,4 - 1 1,4 = 10 0,286 = 1,932

T 2 = 273 + 15 ⋅ 1,932 = 556 K

E fica fácil achar o trabalho no compressor:

w c = h 2 - h 1 = c p ( T 2 - T 1 )

w c = 1,0035 ⋅ 556 - 288 = 269,5 k J k g

Passo 3

Agora vamos fazer a mesma coisa para a turbina:

T 3 T 4 = p 3 p 4 γ - 1 γ

T 3 T 4 = 10 1,4 - 1 1,4 = 10 0,286 = 1,932

T 4 = 273 + 1 100 1,932 = 710 K

E seguindo o mesmo raciocínio

w t = h 3 - h 4 = c p ( T 3 - T 4 )

w t = 1,0035 ⋅ 1373 - 710 = 664,7 k J k g

Passo 4

Agora falta apenas calcular o q h

Pela primeira lei temos que q h = h 3 - h 2 = c p ( T 3 - T 2 )

q h = 1,0035 ⋅ 1373 - 556 = 819,3 k J k g

Passo 5

Substituir na equação da eficiência

η = w l i q q h

η = 664,7 - 269,5 819,3 = 48,2 %

Podemos verificar o resultado utilizando a fórmula

η = 1 - 1 p 2 p 1 γ - 1 γ = 1 - 1 10 0,286 = 48,2 %

Resposta

η = 48,2 %

Exercício Resolvido #7

Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.271 – Exemplo 9.8

Um ciclo ideal a ar Brayton (fechado) opera com entrada no compressor a 0,1 MPa e 15°C. A pressão na saída do compressor é de 1,0 MPa e a temperatura máxima no ciclo é 1100°C. Sabendo que este ciclo é reversível e isotérmico calcule o trabalho consumido no compressor e gerado na turbina. Dado: R a r = 0,287   k g / K

Passo 1

Como os processos são isotérmicos e reversíveis o trabalho pode ser calculado através da equação do trabalho de fluxo

w = - ∫ e s v d p

Que ao utilizar a relação p v γ = c o n s t a n t e pode ser escrito da forma

w = - C ∫ e s d p p = - p e v e ⋅ ln ⁡ p s p e

Utilizando a relação p v = R T

w = - R T e ⋅ l n p s p e

Passo 2

Vamos substituir essa equação no compressor

w c = - 0,287 ⋅ 273 + 15 ⋅ ln ⁡ 10 = - 190,5 k J k g

Passo 3

Agora vamos fazer a mesma coisa para a turbina:

w t = - 0,287 ⋅ 273 + 1100 ⋅ ln ⁡ 0,1 = 907,5 k J k g

É interessante observar que esse exercício trata do mesmo que o anterior, porém de forma reversível e por isso que o trabalho da turbina é superior.

Resposta

w c = - 190,5 k J k g

w t = 907,5 k J k g

Exercício Resolvido #8

Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.295 – Exercício 9.36.

Considere um ciclo padrão a a ar Brayton ideal onde a pressão e a temperatura do ae que entra no compressor são, respectivamente, iguais a 100 KPa e 20°C e a relação de pressão do compressor é de 12 para 1. A temperatura máxima desse ciclo é de 1100°C e a vazão d ar é igual a 10kg/s. Admitindo calor específico constante para o ar igual a c p = 1,0035 k J k g   K e γ = 1,4 . Determine:

a) A eficiência deste ciclo.

b) O trabalho no compressor.

c) O trabalho gerado pela turbina.

Passo 1

Vamos anotar os dados fornecidos pelo problema:

  • Para o compressor temos P 1 = 100   k P a ; T 1 = 20 ° C = 20 + 273 K = 293 K ; P 2 = 12 ⋅ 100 k P a = 1,2 M P a
  • Temperatura máxima do ciclo T 3 = 1100 ° C = 1100 + 273 K = 1373 K
  • m ˙ = 10 k g s
  • c p = 1,0035 k J k g   K
  • γ = 1,4 k J k g   K

Passo 2

Se o problema pediu a eficiência, e deu a relação de pressão no compressor então é só substituir na equação:

η = 1 - 1 P 2 P 1 γ - 1 γ

η = 1 - 1 12 1,4 - 1 1,4 = 1 - 1 12 0,286 = 50,8 %

Passo 3

A potência pode ser calculada como

W ˙ = m ˙ c p Δ T

Então basta saber as temperaturas de entra e saída do compressor para achar a potência. Como já sabemos a temperatura de entrada e temos, também, a relação de compressão podemos utilizar a relação de isentrópicas para achar a temperatura de saída e calcular a potência.

T 2 T 1 = p 2 p 1 γ - 1 γ

T 2 293 = 12 1,4 - 1 1,4

T 2 = 293 ⋅ 12 0,285 = 596 K

Substituindo na equação da potência

W ˙ = m ˙ c p Δ T

W ˙ = 10 ⋅ 1,0035 ⋅ 596 - 293 = 3040   k W

Passo 4

Agora para acharmos a temperatura da turbina utilizaremos o fato das relações entre temperaturas serem iguais:

T 2 T 1 = T 3 T 4

596 293 = 1373 T 4

T 4 = 1373 ⋅ 293 596 = 675 K

Substituindo na equação da potência

W ˙ = m ˙ c p Δ T

W ˙ = 10 ⋅ 1,0035 ⋅ 1373 - 675 = 7004   k W

Resposta

η = 50,8 %

W c ˙ = 10 ⋅ 1,0035 ⋅ 596 - 293 = 3040   k W

W t ˙ = 10 ⋅ 1,0035 ⋅ 1373 - 675 = 7004   k W

Exercícios de Livros Relacionados

Gás argônio inicialmente a 3MPa e 750 ° C é expandido em uma turbina adiabática até 0,2 Mpa, a uma vazão de 5 kg/s. A máxima potência produzida pela turbina é 1,06 MW1,29 MW1,43 kW1,76 MW2,08 MW
Quais são os quatro processos que formam o ciclo Brayton simples ideal?
A seção da turbina em um motor a jato recebe gás (suponha o ar) a 1200 K, 800 kPa com uma atmosfera ambiente a 80 kPa. A turbina é seguida por um bico aberto para a atmosfera e todo o trabalho da turb
Os processos utilizados no ciclo Brayton são iguais àqueles do ciclo Rankine. Porque os diagramas T - s e p - v desses ciclos parecem tão diferentes?
A potência gerada num ciclo de Brayton é 14M W . A relação de compressão utilizada no ciclo é 16 : 1 e o ar entra no compressor a 17° C e 100k P a . Sabendo que o processo de combustão no ciclo pode s