Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Reginaldo - Matrizes, Vetores e Geometria Analítica- Ed: 1º - Capítulo 5.2 - Ex. 5

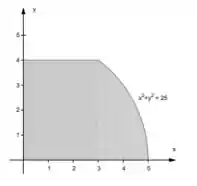
Descreva as regiões a seguir usando coordenadas polares:

Passo 1

Aqui temos que limitar o raio e o ângulo, de acordo com as limitações de x   e   y que temos.

  1. Nesse primeiro desenho, temos o x limitado de 0   a   5 e o y limitado de 0   a   4 . Podemos ver também que é a parte de um círculo de raio 5 .

    2. Então já podemos ver que 0 ≤ r ≤ 5 .

    Temos que a região é delimitada pelo círculo x 2 + y 2 = 25 , pela reta y = 4 ,   y = 0     x = 0 , x = 3 .

    Jogando isso para coordenadas polares:

  • x 2 + y 2 = 25 → r = 5
  • y = 4 → r s e n   θ = 4 → r = 4 sen ⁡ θ
  • y = 0 → r s e n   θ = 0 → θ = 0
  • x = 0 → r cos ⁡ θ = 0 → cos ⁡ θ = 0 → θ = π 2

Temos também uma divisão de ângulos no ponto x = 3 . Onde podemos denotar como:

Como tg ⁡ θ = y x , temos: θ = a r c t g   4 3 .

Unindo essas informações temos a região:

0 ≤ θ ≤   a r c t g   4 3 ,     0 ≤ r ≤ 5 a r c t g   4 3 ≤ θ ≤ π 2 ,         0 ≤ r ≤ 4 sen ⁡ θ  

Passo 2

  • A região é composta por:

    • x 2 + y 2 = 18

    y = 0

    y = 3 2 + x 2   (reta que passa por (-3,0) e (3,3)

    Veja que podemos dividir a figura em duas partes: uma de -3 a 3 e outra de 3 a 3 2 .

    Vamos colocar tudo isso em coordenadas polares:

    • r 2 = 18 → r = 18 = 3 2

    • y = 0 → r s e n   θ = 0 → θ = 0

    • y = 3 2 + x 2 → 2 r sen ⁡ θ = 3 + r cos ⁡ θ → r 2 sen ⁡ θ - cos ⁡ θ = 3 → r = 3 2 sen ⁡ θ - cos ⁡ θ .

    No ponto 3,3 , temos:

    tg ⁡ θ = y x = 3 3 = 1  

    θ = a r c t g   1 = π 4

    Juntando as informações, temos:

    0 ≤ θ ≤ π 4 ,           4 ≤ r ≤ 3 2 π 4 ≤ θ ≤ π ,     0 ≤   r ≤ 3 2 sen ⁡ θ - cos ⁡ θ

    Passo 3

  • Essa região agora é limitada por:

    • x 2 + y 2 = 4

    y = x 2

    y = x

    x = 4

    Passando isso para coordenadas polares:

    • x 2 + y 2 = 4 → r 2 = 4 → r = 2
    • y = x 2 → r sen ⁡ θ = r cos ⁡ θ 2 → sen ⁡ θ = cos ⁡ θ 2
    • tg ⁡ θ = sen ⁡ θ cos ⁡ θ → cos ⁡ θ 2 cos ⁡ θ → tg ⁡ θ = 1 2 → θ = a r c t g   1 2
    • y = x → r sen ⁡ θ = r cos ⁡ θ → sen ⁡ θ = cos ⁡ θ → θ = π 4
    • x = 4 = r cos ⁡ θ → r = 4 cos ⁡ θ

    Unindo essas informações, temos a região dada por:

    a r c t g   1 2 ≤ θ ≤ π 4   ,     2 ≤ r ≤ 4 cos ⁡ θ

    Passo 4

  • Essa região é limitada por:

    • x - 2 2 + y 2 = 4

    y = x 2

    y = 0

    Agora jogamos para coordenadas polares:

    • r 2 cos 2 ⁡ θ - 4 r cos ⁡ θ + 4 + r 2 sen 2 ⁡ θ = 4

      • r 2 cos 2 ⁡ θ + r 2 sen 2 ⁡ θ - 4 r cos ⁡ θ = 0

      r 2 - 4 r cos ⁡ θ = 0

      r r - 4 cos ⁡ θ = 0

      r = 4 cos ⁡ θ

    • y = x 2 → r sen ⁡ θ = r cos ⁡ θ 2 → sen ⁡ θ = cos ⁡ θ 2

      • tg ⁡ θ = sen ⁡ θ cos ⁡ θ → cos ⁡ θ 2 cos ⁡ θ → tg ⁡ θ = 1 2 → θ = a r c t g   1 2

    • y = 0 → θ = π 2

    A região então é dada por:

    a r c t g   1 2 ≤ θ ≤ π 2 ,     0 ≤ r ≤ 4 cos ⁡ θ

    Prontinho! 😉

    Resposta

    1. 0 ≤ θ ≤   a r c t g   4 3 ,     0 ≤ r ≤ 5 a r c t g   4 3 ≤ θ ≤ π 2 ,         0 ≤ r ≤ 4 sen ⁡ θ  
    2. 0 ≤ θ ≤ π 4 ,           4 ≤ r ≤ 3 2 π 4 ≤ θ ≤ π ,     0 ≤   r ≤ 3 2 sen ⁡ θ - cos ⁡ θ
    3. a r c t g   1 2 ≤ θ ≤ π 4   ,     2 ≤ r ≤ 4 cos ⁡ θ
    4. a r c t g   1 2 ≤ θ ≤ π 2 ,     0 ≤ r ≤ 4 cos ⁡ θ

    Exercícios de Livros Relacionados

    A equação da trajetória de uma partícula lançada do ponto P 0 = ( 0,0 ) , com velocidade v 0 , fazendo um ângulo α com o eixo x e sujeita apenas a ação da aceleração da gravidade g é dada por y = t g
    Se a cônica de equação r = d e 1 - e cos ⁡ θ representa uma elipse, mostre que o comprimento do seu eixo menor é 2 d e 1 - e 2 .
    Mostre que a equação em coordenadas polares de uma elipse com um dos focos no polo, que tem eixo maior igual à 2 a e excentricidade e é r = a 1 - e 2 1 - e cos ⁡ θ
    Descreva o conjunto representado, em coordenadas polares, pela equação R = 3 s i n θ
    Esboce o conjunto dos pontos do plano cujas coordenadas polares satisfazem a relação R = cos ⁡ 3 θ