Uma partícula desloca-se ao longe de um ramo da hipérbole com velocidade, em cada ponto , igual ao vetor tangente nesse ponto. Obtenha os valores máximo e mínimo da velocidade escalar da partícula em função dos parâmetros geométricos e , e os pontos em que esses valores são atingidos.
Passo 1
Primeiro de tudo, se lembrarmos como é a estrutura de uma hipérbole, vamos de cara supor que não encontraremos um valor máximo e isso é verdade. Já para o valor mínimo será atingido no vértice da hipérbole, seu valor vai ser dado por e para chegar nesse valor devemos lembrar quem são esses componentes na nossa hipérbole e para isso vamos utilizar uma imagem
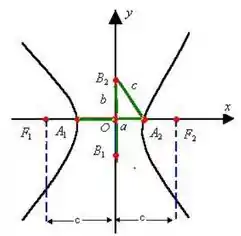
Devemos fazer algumas manipulações algébricas para encontrarmos o valor dessa velocidade mínima, além de aplicarmos as equações relacionadas à velocidade.
Resposta
Velocidade mínima será e Velocidade máxima: não tem.