Exercícios de Hipérboles - Lista de Exercícios Resolvida
Questão 1
Determine os vértices, os focos, a excentricidade e as assíntotas das hipérboles dadas a seguir. Faça um esboço.
Questão 2
Determinar o centro, um esboço do gráfico, os vértices e os focos da hipérbole de equação:
Ver solução completaQuestão 3
Achar a equação da hipérbole centrada na origem com focos nos pontos e e que passa pelo ponto .
Ver solução completaQuestão 4
Seja o lugar geométrica dos pontos do plano cujas coordenadas e satisfazem
- Qual o tipo da cônica ? Escrever a equação canônica de .
- Encontrar os focos, os vértices e a excentricidade de . No caso de hipérbole, encontrar também as equações das assíntotas no sistema .
Questão 5
Nas cônicas da figura os focos da hipérbole são vértices da elipse, os focos da elipse são vértices da hipérbole e o foco da parábola é um vértice da elipse. Sabendo que a equação da elipse é
determine as equações da parábola e da hipérbole.
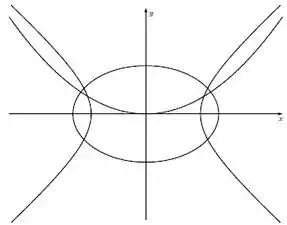
Questão 6
No plano , considere o ponto e a reta , mostre que o lugar geométrico dos pontos tais que é uma cônica.
- Identifique .
- Determine os parâmetros geométricos de .
- Determine a excentricidade de .
- Faça um esboço de .
Questão 7
Seja uma hipérbole com focos sobre o eixo , centro na origem e eixo transverso (distância entre os vértices) 10. Sabendo que o ponto , determine a equação reduzida, as coordenadas dos focos e vértices e as equações das assíntotas de .
Ver solução completa