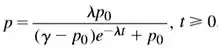Enunciado
Cálculo - Guidorizzi - Vol. 4 - Ed: 5º - Capítulo 10.5 - Ex. 3a
Considerando fatores inibidores para a variação da população, foi proposta uma modificação para o modelo do exercício anterior, onde se supõe então um nível máximo que a população possa atingir e que há um fator inibidor proporcional ao quadrado da população e com coeficiente . Então, neste modelo, a variação da população é regida pela equação de Bernoulli , onde se supõe . Suponha que a população no instante seja .
- Resolva a equação
Passo 1
Vamos lá! A equação é uma equação de Bernoulli e, também, de variáveis separáveis.
Passo 2
Resolvendo-a obtemos
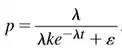
Tendo em vista a condição e , resulta:
