Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.6 - Ex. 4
Determine a área da superfície.
A parte da superfície que está acima do triângulo com vértices , e .
Passo 1
E aiiiiii pessoal, tudo bem com vocês?
Bom, precisamos determinar a área da superfície que compreende parte da superfície:
e está acima do triangulo de vértices:
Vish, e agora?
Precisamos lembrar primeiramente como calculamos a área de uma superfície. Para isto, basta resolver a seguinte integral:
Onde, .
Observe que temos derivadas parciais de uma função . Olhando para as equações fornecidas, já temos a função de que dependa de e . Que é:
E os vértices do triangulo? Vamos precisar fazer um esboço dessa região. Logo, vamos concluir que se trata de uma região do tipo I ou II.
Vamos lembrar como é a região tipo I e II.
Tipo I:
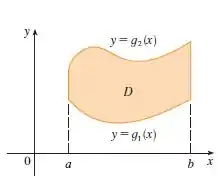
Tipo II:
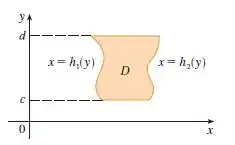
Depois disso e só aplicar na integral e começar a resolver. Lembre-se, que sempre começamos a integrar de dentro para fora.
Vamos começar!
Passo 2
Precisamos lembrar primeiramente como calculamos a área de uma superfície. Para isto, basta resolver a seguinte integral:
Onde, .
Portanto, precisamos calcular primeiramente as derivadas parciais de em função de e de para só depois resolvermos as integrais.
Sabemos também quem é , pois o enunciado forneceu:
Logo, as derivadas parciais da função vão ser:
Portanto, devemos resolver a seguinte integral:
Simplificando:
Passo 3
Vamos avaliar a região delimitada pelo triangulo de vértices:
A nossa região pode ser visualizada abaixo:
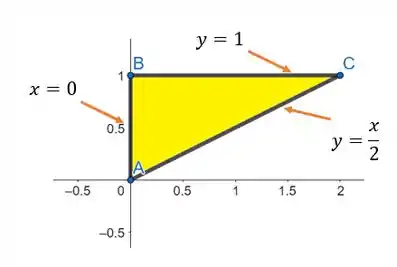
A região pode ser descrita como tanto do tipo I quanto do tipo II. Devido à presença de uma função de dentro da raiz, a integral se torna mais fácil de ser resolvida se descrevermos a região como sendo do tipo II.
Portanto,
Passo 4
Agora, só nos basta aplicarmos os limites de integração e resolvermos a integral.
Vamos ter a seguinte integral:
Começamos resolvendo de dentro para fora. Logo, integrando em vamos ter:
Aplicando os limites de integração:
Agora, pra resolver essa integralzinha vamos fazer a seguinte substituição:
Também vamos escrever os limites de integração em função de . Vamos ter:
Assim, a integral fica:
Integrando em , temos:
Aplicando os limites de integração e simplificando, vamos ter:
Show ein pessoal, encontramos nossa resposta!!! Uhuuuullll