Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.1 - Ex. 50
Enconctre o domínio e esboce o gráfico da função:
Passo 1
Eaaee jovem, vamos matar mais essa questãozinha aqui. Vem comigo!
Lembra como a gente determina o domínio?? Esse cara nada mais é do que os valores possíveis de . Ou seja, quais valores de nos dá um valor em .
Passo 2
Olhando para a nossa questão:
Você consegue perceber que o domínio desse cara é todo o conjunto dos Reais?? Agora vamos analisar as limitações de cada curva:
Por um lado o domínio dessa reta é os reais, ou seja , mas como deve ser menor que , teremos então:
Isso significa que a função pode assumir valores de postivos até o infinito e para valores positivos ele não pode assumir valores iguais ou menores que !
Agora vamos para a segunda reta, . A sua limitação é , podemos abrir esse módulo:
Toda vez que estiver nesse intervalo .
E também existe um valor para quando .
Então note que pode ser qualquer Real. Portanto:
Passo 3
Para esboçar o gráfico, podemos tomar alguns pontos especiais.
Chegaremos em algo mais ou menos assim:
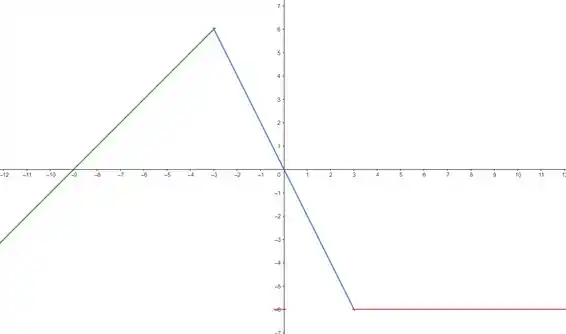
E isso é tudo por enquanto!! Até a próxima!
Resposta
Concluindo, o domínio de é o conjunto de todos os Reais.