Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 6c

Esboce o gráfico:

f (x) = ||x| - 1|

Passo 1

Como temos uma função com módulo dentro de um módulo, devemos estudar sua lei por meio da definição do modulo sendo ela: |x| = x se x >= 0 e |x| = - x se x < 0 , ou seja, para um valor positivo dentro do módulo mantemos o sinal ao tirar do módulo e para um valor negativo dentro do módulo trocamos o sinal e tiramos o módulo. Mas para que para esse caso devemos estudar os módulos internos e externos separadamente.

Passo 2

Assim:

Para x >= 0 :

f (x) = ||x| - 1| = |x - 1|

f (x) = |x - 1|

Nesse casso ainda temos para 0 <= x <= 1 que |x - 1| = - (x - 1) = - x + 1 e para x > 1 que |x - 1| = x - 1

Portanto:

f (x) = {[[- x + 1 s e 0 <= x <= 1],[x - 1 s e x > 1]])

Para x < 0 :

f (x) = ||x| - 1| = |- x - 1|

f (x) = |- x - 1|

Nesse casso ainda temos para x <= - 1 que |- x - 1| = - x - 1 e para - 1 < x < 0 que |- x - 1| = - (- x - 1) = x + 1

Portanto:

f (x) = {[[- x - 1 s e x <= - 1],[x + 1 s e - 1 < x < 0]])

Passo 3

Reunindo as informações temos:

f (x) = {[[- x - 1 s e x <= - 1],[x + 1 s e - 1 < x < 0],[- x + 1 s e 0 <= x <= 1],[x - 1 s e x > 1]])

Assim, o gráfico de f é obtido tracando as quatro retas:

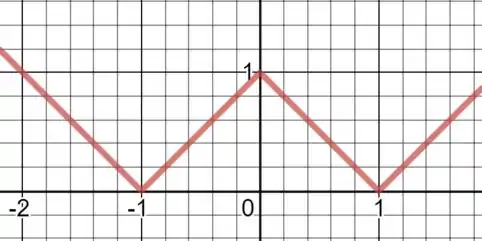
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce o gráfico:f (x) = |x| - 1
Esboce o gráfico:f (x) = |x| + |x - 2|
Esboce o gráfico:f (x) = |x + 1| - |x|
Encontre o domínio e esboce o gráfico da função g x = x - x .