Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.Revisão - Ex. 56
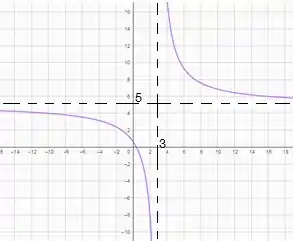
Nos exercícios 55 e 56, ache as assíntotas horizontais e verticais e trace um esboço do gráfico da equação.
56)
Passo 1
O primeiro para será isolar y na equação dada:
Passo 2
As assíntotas horizontais são obtidas quando fazemos x tender a mais infinito e a menos infinito.
Lembrando que, limites de funções polinomiais quando x tende a infinito, tomamos o termo dominante no numerador e no denominador.
Portanto, teremos uma assíntota horizontal em .
Passo 3
As assíntotas verticais são obtidas calculando os limites laterais nas restrições do domínio da função.
O domínio da função é:
Calcularemos os limites a direita e esquerda do 3:
Portanto, teremos uma assíntota vertical em .
Passo 4
O gráfico da função será:
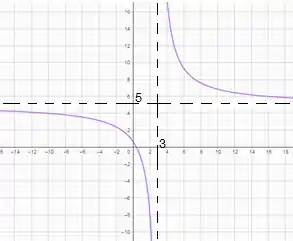
Resposta
Assíntota vertical:
Assíntota horizontal:
Gráfico da função:
Exercícios de Livros Relacionados
Analisar graficamente a existência de assíntotas para as seguintes funções: f x = x 2 e x
Analisar graficamente a existência de assíntotas para as seguintes funções: f x = s e n π x
Fazer o gráfico das funções seguintes e determinar os respectivos limites. Para melhor visualização, traçar, também, o gráfico das retas indicadas. A seguir, determinar analiticamente os limites dados
Determinar as assíntotas horizontais e verticais do gráfico da seguinte função: f x = 4 x 2 - 3 x + 2
Determinar as assíntotas horizontais e verticais do gráfico da seguinte função: f x = 2 x 2 x 2 - 16