Prove que um gráfico simétrico com respeito a duas retas perpendiculares quaisquer também seja simétrico com relação ao ponto de intersecção delas.
Passo 1
Sabemos que o gráfico é simétrico em relação a uma reta r e em relação a uma reta s perpendicular à reta r. Precisamos descobrir se ele é simétrico em relação à interseção das duas.
Passo 2
Para um gráfico ser simétrico em relação a uma reta r, é preciso que, para todo ponto A pertencente ao seu gráfico, exista um ponto B também pertencente ao gráfico tal que a reta r seja mediatriz do segmento (ou seja, ela divide o segmento ao meio e é perpendicular a ele).
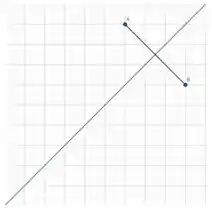
Passo 3
Agora repetimos o passo 2 para a reta s: para todo ponto A pertencente ao gráfico, temos um ponto C que também pertence ao gráfico e é tal que a reta s é mediatriz do segmento .
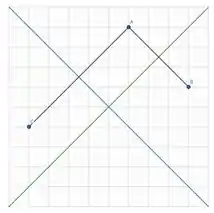
Passo 4
Se o gráfico é simétrico em relação à reta r (verde), então há um ponto D do gráfico tal que a reta r seja mediatriz do segmento
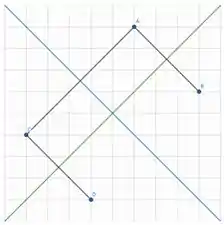
E se o gráfico é simétrico em relação à reta s (azul), então há um ponto E do gráfico tal que a reta s seja mediatriz do segmento .
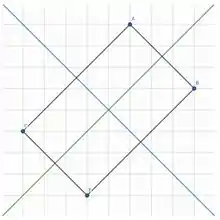
E podemos ver que .
Passo 5
Sabemos que o ponto E pertence ao gráfico pelos passos anteriores. Agora basta sabermos se ele é o simétrico de A com relação ao ponto O:
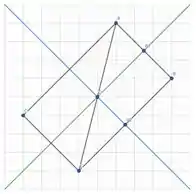
Por construção, as retas são perpendiculares entre si e em relação aos segmentos, então o ângulo é perpendicular também. E como o ângulo e o ângulo , temos que os triângulos são semelhantes.
Como a reta r é mediatriz do segmento , o ponto divide o segmento em duas partes iguais, então a razão de semelhança entre e é .
Sabemos também que a reta s é mediatriz do segmento , então o ponto divide o segmento em duas partes iguais e assim a razão de semelhança entre e é também.
Assim, os triângulos são iguais. Logo os segmentos e são iguais e, dessa forma, o ponto O divide o segmento em duas partes iguais.
Portanto o ponto E é o simétrico de A em relação ao ponto O de interseção das retas.
Resposta
Ei, a resposta está no passo a passo :)