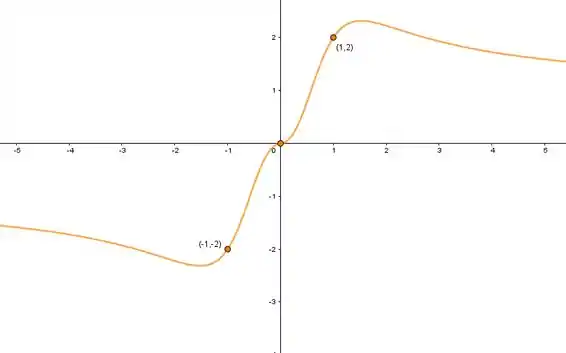
Trace o gráfico de uma função que satisfaça as condições dadas.
, e
Passo 1
O primeiro passo é olhar o tipo de resposta que o limite apresenta, ou seja, se zero, um número ou . Com isso, nós podemos ver qual tipo de função se encaixa melhor para cada caso.

Na questão temos que, e , isso significa que uma divisão de polinômios de mesmo grau, cairia bem já que nesses casos, quando o limite dará um número. Veja no exemplo abaixo:
Passo 2
O segundo passo é lembra que ,, isso nos faz lembrar que essa função não pode ser definida de qualquer jeito, então quando formos definir a cara dela precisamos coloca-la de um jeito que a substituição de e fique simples.
Passo 3
O terceiro passo é perceber que o limite dessa função assume valores diferentes quando e quando , então vamos separar o problema em duas partes, ou seja, vamos imaginar a cara da função quando e quando .
Para isso vamos ver que a cara da quando , sabendo que ela tem que ser uma divisão de polinômios de mesmo grau e que quando , .
Então quando podemos pensar em escrever assim:
O que é TOP pois,
Como estamos com polinômios, vamos dividir o numerador e o denominador pela maior potência de x,
Usando a regra do quociente (o limite do quociente é o quociente dos limites) e da subtração (o limite da subtração é a subtração dos limites),
E
E como 1 não está no domínio, então não temos com o que nos preocupar.
Mas ainda tem os valores que assume quando , e nessa situação sabemos que , que tem que ser uma divisão de polinômios de mesmo grau e que quando , .
Então quando podemos pensar em escrever assim:
Isso é legal porque, usando as mesmas regras que usamos anteriormente,
E,
E como não está no intervalo que estamos consideramos, então não temos com o que nos preocupar. Além disso, independentemente do valor de vamos encontrar que
E portanto,
Resposta