Fadiga

Vimos que materiais sofrem falha por fadiga quando submetidos a carregamentos cíclicos. Mas afinal, o que são carregamentos cíclicos?

Carregamento cíclico é quando um material sofre esforços entre níveis constantes de tensão máxima e mínima. Como ilustrado abaixo.

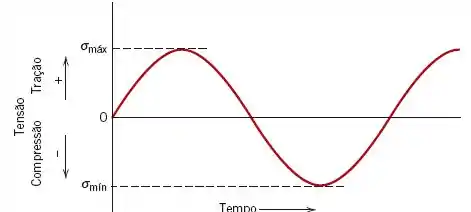
Note que o carregamento varia com o tempo entre o nível de tensão máximo e o nível de tensão mínimo e sua amplitude permanece constante.

A faixa de tensões, , é a diferença entre os valores máximos e mínimo. A média entre os valores máximos e mínimos é a tensão média,. A tensão média pode ser zero, como na figura acima, mas muitas vezes não o é, como na figura abaixo.

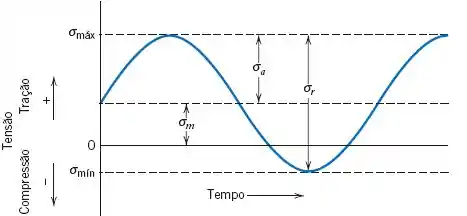
A metade da faixa de tensões é conhecida como amplitude de tensões, , que nada mais é do que a variação em torno da média.

O termo tensão alternada é usado por alguns autores e tem o mesmo significado de amplitude de tensão.

Manipulando algebricamente as equações acima obtém-se:

,

Note que os sinais de e são sempre positivos, uma vez que .

Às vezes, as seguintes razões são empregadas:

Onde, é chamada razões entre tensões e , razão de amplitude. Algumas relações adicionais, derivadas das equações anteriores, também são úteis:

Um carregamento cíclico com média nula pode ser especificado pela amplitude de tensões, ,ou pelo valor da tensão máxima, , que é numericamente igual à amplitude de tensões. Como podemos checar na curva abaixo.

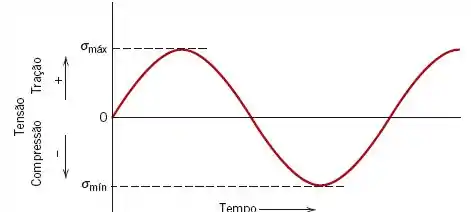
Na figura acima temos:

Caso a tensão média não seja nula, dois valores independentes são necessários para especificar o carregamento.

O termo carregamento cíclico completamente reverso é usado para descrever uma situação na qual ou , como dá figura acima. Além disso, um ciclo de mínimo nulo refere-se a casos em que ou .

O mesmo sistema subscritos (e do prefixo ) é usado de maneira análoga para outras variáveis, tais como deformação , força , momento de flexão e tensão nominal . Por exemplo, e são as forças máximas e mínimas, é a faixa de forças, é a força média e é a amplitude de força. Se há qualquer possibilidade de confusão quando essas variáveis são empregadas para definir as razões ou , emprega-se um subscrito para evitar este problema, como no caso de para designar a relação entre deformações.

Tensões Pontual versus Tensão Nominal

É importante diferencial entre a tensão em um ponto, , e a tensão nominal ou média, , e por esta razão, usamos dois símbolos distintos. A tensão nominal é calculada a partir da força, do momento ou de sua combinação, sendo que por uma questão de conveniência somente é igual a em certas situações.

Vamos praticar uma pouco?