Considere um componente de aço inoxidável - Mo (Figura ) que está exposto a uma temperatura de . Qual é o nível máximo de tensão admissível para um tempo de vida útil até a ruptura de anos? E para anos?

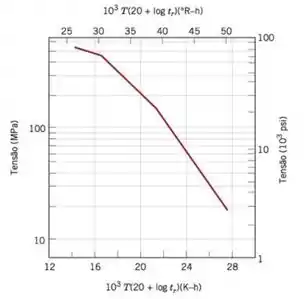
Figura Logaritmo da tensão em função do parâmetro de Larson-Miller para um aço inoxidável - Mo.

Olá! Tudo bem? Neste problema, devemos calcular os níveis de tensão nos quais o nível máximo de tensão admissível para um tempo de vida útil até a ruptura de anos e anos, quando um componente de aço inoxidável - Mo for submetido a uma temperatura de .

Primeiro, devemos calcular o valor do parâmetro Larson-Miller para cada tempo. Os valores de correspondentes a e anos são e , respectivamente.

Assim, para um tempo de anos, temos:

E para , temos:

Usando a curva mostrada na Figura , os valores de tensão correspondentes aos tempos de vida útil até a ruptura de anos e anos são de aproximadamente e , respectivamente.