Teorema de Thévenin e Norton
Produzido por Alexandre NunesTeoria
Fala aí, tudo certo? Hoje nós vamos aprender sobre o Teorema de Thévenin e o Teorema de Norton.
Esses caras vão nos fornecer ferramentas para nos ajudar na análise de circuitos elétricos mais complexos por meio do conceito de circuitos equivalentes. Para você ter uma ideia, no final do texto nós vamos ser capazes de transformar este circuito aqui:
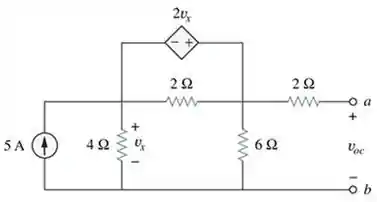
Neste circuito bem mais fofinho:
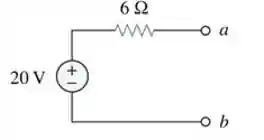
Ah, relevante: tem alguns assuntos que são bem importante você estar por dentro antes de darmos sequência nisso aqui, então vou deixar uns links que podem ser bacanas se você precisar dar uma revisada 😉👇
Teorema de Thévenin
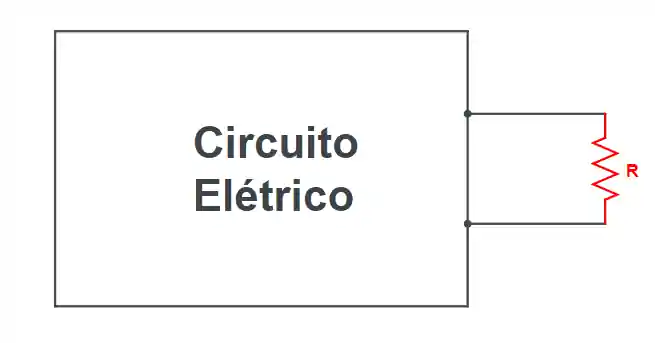
O Teorema de Thévenin fala que um circuito linear conectado a um par de terminais qualquer pode sempre ser representado por uma fonte de tensão com resistência interna. Não entendeu? Deixa eu desenhar, imagina um sistema desse modelo:
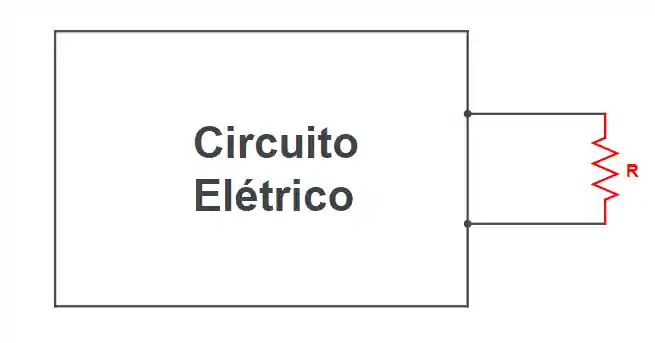
O que tá dentro dessa caixa escrito “Circuito Elétrico” não interessa muito, pode ser algo parecido com aquele sistema lá do começo, por exemplo. Enfim, o Teorema tá nos falando que podemos pegar tudo o que estiver lá dentro e substituir por algo bem mais simples e equivalente, assim:
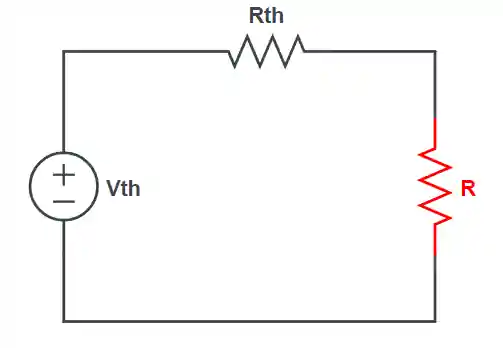
Do ponto de vista daquela resistência R em vermelho, aquela fonte
Modelo Equivalente de Thévenin
Para encontrar os valores de
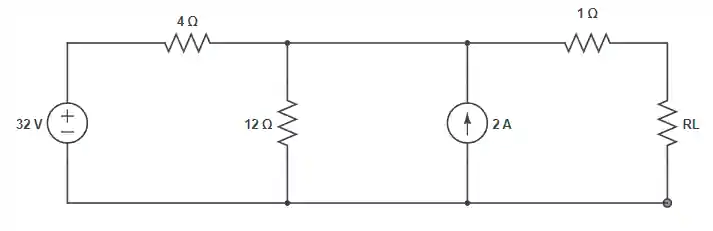
- O primeiro passo é identificar para que parte será feita a análise e que parte será substituída pelo circuito equivalente de Thévenin.
Neste caso, queremos levantar o modelo para aquela resistênciaali na direita, quer dizer que todo o restante vai ser substituído. - Segundo, vamos abrir o circuito lá no ponto identificado e encontrar a tensão de circuito aberto.
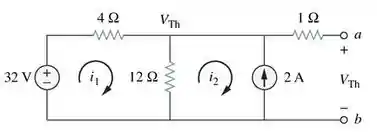
Circuito aberto para o cálculo da tensão equivalente. Vamos começar aplicando a Lei de Kirchhoff das Tensões ali na primeira malha:
Ali da segunda malha, tiramos que
. Então, se substituirmos esse valor na equação anterior e resolver para , vamos encontrar o seguinte: Como o terminal a está aberto, não passa nenhuma corrente por aquele resistor de
. Com isso, sabemos que o terminal está em paralelo com o resistor de . Quer dizer que eles têm a mesma tensão, então:
- Beleza, terceiro: vamos provocar um curto-circuito em todas as fontes independentes de tensão e abrir todas as fontes independentes de corrente. Assim poderemos calcular a resistência equivalente
vista pelos terminais .
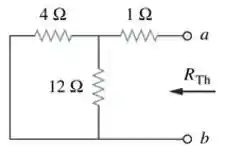
Circuito para o cálculo da resistência equivalente. - Pra finalizar, desenhamos o circuito equivalente de Thévenin com os valores que encontramos.
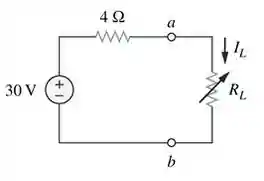
Agora que temos esse circuito equivalente, podemos substituir qualquer valor em
Teorema de Norton
O Teorema de Norton fala que um circuito linear conectado a um par de terminais qualquer pode ser substituído por uma fonte de corrente em paralelo com um resistor. Ou seja, aquele mesmo circuito genérico:
Dessa vez vai ser trocado por algo do tipo:
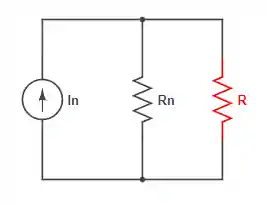
E para fazer isso não tem muito segredo não. O primeiro passo é perceber uma equivalência entre os modelos de Thévenin e de Norton. Se liga, quando temos sistemas como os seguintes:
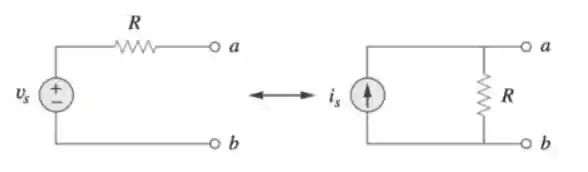
Podemos fazer um processo conhecido como transformação de fontes, que consiste em substituir uma fonte de tensão
E por que isso é relevante? Ora, não reparou como esses circuitinhos aí são os próprios modelos de Thévenin (à esquerda) e de Norton (à direita)? Isso quer dizer duas coisas:
- O cálculo de
é exatamente igual ao cálculo de . - A corrente de Norton
pode ser dada por:
Então, um meio de encontrar o circuito equivalente de Norton é simplesmente encontrar o de Thévenin primeiro, e então usar a transformação de fontes para fazer a conversão. Mas, claro, se você quiser ir direto para o de Norton, tem uma outra saída.
Para encontrar a resistência
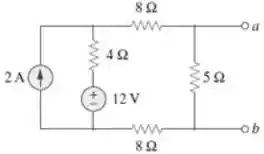
Primeiro, vamos provocar um curto-circuito nos terminais
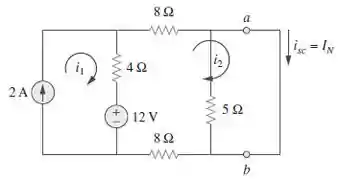
Com isso, podemos desconsiderar aquele resistor de
E, como
E, olhando para o circuito, podemos perceber que a corrente
Beleza, agora você pode sempre escolher começar pelo modelo de Thévenin e, a partir dele, encontrar o de Norton, ou fazer o caminho oposto, dependendo do que você achar mais fácil 😁
Bora praticar com alguns exercícios pra ajudar a fixar tudo isso aí!!