Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Indutores

Ver Todos os Exercícios

Teoria

E aí, tá animado? Agora que a gente já está fera em capacitor, vamos estudar sobre outro elemento passivo, o indutor.

O indutor nada mais é que uma bobina com várias espiras de fio condutor e é projetado para armazenar energia em seu campo magnético. Eles são muito utilizados em transformadores e motores.

Estrutura física

Como eu falei, os indutores normalmente são formados por uma bobina cilíndrica enrolada por várias espiras de fio condutor.

Agora, vamos supor que uma corrente elétrica passa pelo indutor que possui a simbologia da figura abaixo:

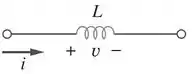
Quando isso ocorre, a tensão no indutor é diretamente proporcional a taxa variação da corrente que circula nele, ou seja:

v = L d i d t

Onde L é chamada a indutância do indutor e é medida em henrys (H).

Pela equação, a gente vê que a 1 henry corresponde a 1 volt-segundo por ampère.

Indutância

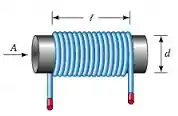
Os indutores apresentam diferentes dimensões e podem ser constituídos de diversos materiais. Na imagem abaixo eu separei alguns tipos.

A indutância depende exatamente disso. Da estrutura física do indutor e do seu material. Assim como os capacitores, os indutores possuem diferentes valores típicos. Então, por exemplo, no caso do indutor de ferro na forma de solenoide a indutância L é dada por:

L = µ N 2 A l

Enquanto os valores de N ,   l   e   A variam com a construção do indutor, o valor de μ varia de acordo com o material utilizado no indutor. A permeabilidade magnética do núcleo é uma propriedade que varia de material para material.

Os valores comerciais mais encontrados para indutância variam de poucos microhenrys ( μ H ) a dezenas de henrys (H).

Relações importantes nos indutores

A gente já sabe a relação entre tensão e corrente no indutor:

v = L d i d t

Agora, vamos deixar a corrente isolada na equação acima.

d i = 1 L v   d t

Integrando os dois lados:

i = 1 L ∫ t 0 t v   d t + i t 0

Pronto, essa é a relação entre corrente e tensão em um indutor.

Sabendo essas relações podemos obter as equações de potência e energia de um Indutor.

Para potência, temos:

P = v i

P = L d i d t i

Logo, a energia armazenada será:

w = ∫ t 0 t P   d t

w = ∫ - ∞ t   L i d i d t d t

w =   L ∫ t 0 t i   d i

w = 1 2 L i 2 t - 1 2 L i 2 t 0

Considerando que não circula corrente no indutor em t 0 :

w = 1 2 L i 2

Você já deve ter percebido que capacitores e indutores têm uma relação de dualidade. Ou seja, as relações e propriedades em um indutor são inversas ao do capacitor.

Lembra que um capacitor é um circuito aberto para tensão contínua? Já o indutor, adivinha, será um curto-circuito em CC.

Lembra, também, da propriedade que a tensão no capacitor não pode variar instantaneamente? No indutor, o que não pode variar instantaneamente é a corrente!

Maneiro né?!

Associação de indutores

Vamos supor que a gente tenha o circuito abaixo, com indutores associados em série:

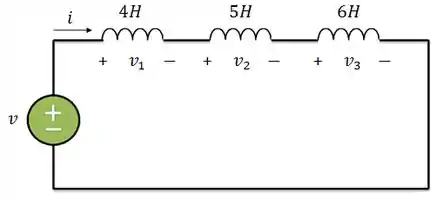
Aplicando a LTK:

v = v 1 + v 2 + v 3

Pela relação de tensão no indutor:

v 1 = 4 d i d t

v 2 = 5 d i d t

v 3 = 6 d i d t

Substituindo:

v = 4 d i d t + 5 d i d t + 6 d i d t

v = 4 + 5 + 6 d i d t  

v = 15 d i d t  

Logo,

L e q = 4 + 5 + 6 = 15   H

Então, quando os indutores estão em série, a indutância equivalente é a soma das indutâncias de cada indutor.

L e q = L 1 + L 2 + L 3 + … + L N

Agora, vamos ver quando os indutores estão associados em paralelo. Como no circuito abaixo:

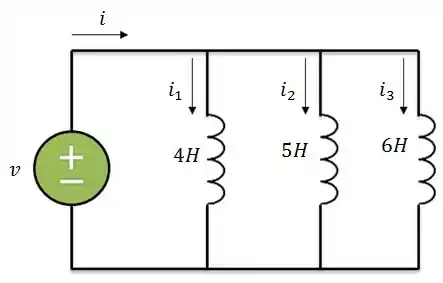
Aplicando LCK:

i = i 1 + i 2 + i 3

Pela relação de corrente no indutor:

i 1 = 1 4   ∫ t 0 t v   d t + i 1 ( t 0 )  

i 2 = 1 5   ∫ t 0 t v   d t + i 2 ( t 0 )

i 3 = 1 6   ∫ t 0 t v   d t + i 3 ( t 0 )

Substituindo:

i = 1 4   ∫ t 0 t v   d t + i 1 ( t 0 ) + 1 5   ∫ t 0 t v   d t + i 2 ( t 0 ) + 1 6   ∫ t 0 t v   d t + i 3 ( t 0 )

i = 1 4 + 1 5 + 1 6 ∫ - ∞ t v   d t + i 1 ( t 0 ) + i 2 t 0 + i 3 t 0

i = 37 60 ∫ t 0 t v   d t + i ( t 0 )

Logo,

1 L e q = 1 4 + 1 5 + 1 6 = 37 60

Então, quando os indutores estão associados em paralelo, a indutância equivalente é o inverso da soma dos inversos das indutâncias de cada indutor.

1 L e q = 1 L 1 + 1 L 2 + 1 L 3 + … + 1 L N

Se a gente puxar na memória, notamos que os indutores em paralelo se associam da mesma forma que os resistores em paralelo. Então, para a associação de dois indutores em paralelo temos aquela velha fórmula do produto sobre a soma:

L e q = L 1 L 2 L 1 + L 2

Não pode faltar aquele resumão maneiro para indutores.

Agora é fazer exercício para fixar!

Relações importantes nos indutores

Associação de indutores

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

Calcule a indutância de uma bobina cujas características são:

  • 1000 espiras
  • Comprimento igual a 10cm
  • Área transversal igual a 5 c m 2
  • Permeabilidade igual a do ar

Passo 1

A indutância calculada de acordo com as características físicas do indutor segue a seguinte fórmula:

L = µ *   N 2 * A l

Passo 2

Para o caso da permeabilidade ser igual a do ar,

µ = 4 * π * 10 - 7 .

N   =   1000

l = 10 c m = 0,1 m

A = 5 c m 2 = 0,0005 m 2

Passo 3

L = 4 * π * 10 - 7 * 10 6 * 0,0005 0,1 = 6,28 m H

Resposta

L = 6,28 m H

Exercício Resolvido #2

Livro Sadiku, 5ª edição, p.217, Problema 6.35

Um indutor possui uma mudança linear na corrente variando de 50   m A a 100   m A em 2   m s e induz uma tensão de 160   m V . Calcule o valor do indutor.

Passo 1

Primeiro, o enunciado diz que a corrente varia de 50   m A a 100   m A em 2   m s , ou seja:

d i d t = ( 100 - 50 ) × 10 - 3 2 × 10 - 3 = 25

E depois que

v = 160   m V

Passo 2

A gente precisa encontrar a indutância. Vamos isolar L na equação abaixo:

v = L d i d t  

L = v d i d t

Passo 3

Substituindo os dados do enunciado:

L = 160 × 10 - 3 25

L = 6,4   m H

Resposta

L = 6,4   m H

Exercício Resolvido #3

Livro Sadiku, 5ª edição, p.217, Problema 6.34

A corrente através de um indutor de 10   m H é 10   e - t 2     A . Determine a tensão e a potência em t = 3   s .

Passo 1

Primeiro, vamos ver os dados que o enunciado nos fornece:

L = 10   m H

i = 10   e - t 2     A

Passo 2

Agora vamos calcular a tensão. Sabemos que a tensão em um indutor tem a seguinte relação:

v = L d i d t  

Substituindo os dados do enunciado:

v = ( 10 × 10 - 3 ) d d t 10 e - t 2

Passo 3

Precisamos resolver a derivada. Pela regra da cadeia, temos:

d d t 10   e - t 2 = 10 e - t 2 × - 1 2

d d t 10   e - t 2 = - 5 e - t 2

Passo 4

Agora, vamos substituir na equação da tensão.

v = 10 × 10 - 3 - 5 e - t 2

v ( t ) = - 0,05 e - t 2   V

Passo 5

Quando t = 3   s , temos:

v 3 = - 0,05 e - 3 2

v 3 = - 11,16   m V

Passo 6

Falta determinarmos a potência. Sabemos que:

P = v i

Substituindo os valores:

P = - 0,05 e - t 2 10   e - t 2

P t = - 0,5 e - t   W

Passo 7

Então, a potência quando t = 3   s será:

P 3 = - 0,5 e - ( 3 )  

P 3 = - 24,89   m W

Resposta

v 3 = - 11,16   m V

P 3 = - 24,89   m W

Exercício Resolvido #4

Livro Sadiku, 5ª edição, p.217, Problema 6.39

A tensão em um indutor de 20 0   m H é dada por

v t = 3 t 2 + 2 t + 4   V   p a r a   t > 0 .

Determine a corrente i t que passa pelo indutor. Suponha que i ( 0 ) = 1   A .

Passo 1

Primeiro, vamos ver os dados que o enunciado nos fornece:

L = 20 0   m H

v t = 3 t 2 + 2 t + 4   V

i ( 0 ) = 1   A

Passo 2

Agora, com esses dados, precisamos encontrar a corrente que passa pelo indutor. Sabemos que a corrente em um indutor tem a seguinte relação:

i = 1 L ∫ t 0 t v t d t + i ( t 0 )  

Como t 0 = 0 , temos

i = 1 L ∫ 0 t v t d t + i ( 0 )

Passo 3

Substituindo os dados do enunciado:

i = 1 200 × 10 - 3 ∫ 0 t 3 t 2 + 2 t + 4   d t + 1

Passo 4

Agora, vamos resolver a integral separadamente.

∫ 0 t 3 t 2 + 2 t + 4   d t = 3 t 3 3 + 2 t 2 2 + 4 t   t 0

∫ 0 t 3 t 2 + 2 t + 4   d t = t 3 + t 2 + 4 t

Passo 5

Substituindo na equação da corrente:

i = 1 200 × 10 - 3 t 3 + t 2 + 4 t + 1

Simplificando:

i t = 5 t 3 + 5 t 2 + 20 t + 1   A

Resposta

i t = 5 t 3 + 5 t 2 + 20 t + 1   A

Exercício Resolvido #5

Livro Sadiku, 5ª edição, p.218, Problema 6.48

Em condições de CC de regime estacionário, determine i e v no circuito abaixo.

Passo 1

A gente já tinha visto que o capacitor em CC é um circuito aberto e, também, vimos na teoria de indutores que o indutor é um curto-circuito. Então vamos redesenhar o circuito.

Passo 2

A corrente só circula em caminhos fechados. Logo, a corrente i passa totalmente pelo resistor de 20   k Ω e a tensão v é a tensão aplicada nesse resistor.

Aplicando divisor de corrente, temos:

i = 30 × 10 3 30 + 20 × 10 3   ( 5 × 10 - 3 )

i = 3   m A

Passo 3

Agora é só aplicar a lei de Ohm e correr pro abraço:

v = 20 k i

v = 20 × 10 3 3 × 10 - 3

v = 60   V

Resposta

i = 3   m A

v = 60   V

Exercício Resolvido #6

Livro Sadiku, 5ª edição, p.218, Problema 6.46

Determine v c , i L e a energia armazenada no capacitor e indutor no circuito abaixo em condições de CC.

Passo 1

Como a gente viu o capacitor em CC é um circuito aberto e o indutor é um curto-circuito. Então, vamos redesenhar o circuito.

Passo 2

A corrente só circula em caminhos fechados. Logo, ela não passa pelo resistor de 5   Ω e a tensão v c e a corrente i L podem ser obtidas conforme no circuito abaixo:

Tá lembrado de divisor de corrente? Vamos usar aqui:

i L = 4 2 + 4 3 = 2   A

i 1 = 2 4 + 2 3 = 1   A

Passo 3

Aplicando a lei de Ohm, temos:

v 1 = 4 i 1 = 4   V

v 2 = 2 i L = 4   V

Aplicando a LTK:

- v 1 + v 2 + v c = 0

v c = v 1 - v 2

v c = 4 - 4 = 0   V

Passo 4

Agora que já calculamos v c e i L , vamos calcular a energia armazenada nos elementos.

Primeiro no capacitor:

w C = 1 2 C v c 2

w C = 1 2 2 0 2 = 0   J

Agora no indutor:

w L = 1 2 L i L 2

w L = 1 2 0,5 2 2

w L = 1   J

Resposta

v c = 0   V

i L = 2   A

w C = 0   J

w L = 1   J

Exercício Resolvido #7

Livro Sadiku, 5ª edição, p.218, Problema 6.51

Determine a L e q nos terminais a - b do circuito da figura abaixo.

Passo 1

A gente viu que os indutores se associam da mesma forma do que os resistores. Vamos começar pelos indutores de 60   m H , 20   m H e 30   m H que estão em paralelo:

1 L e q 1 = 1 60 + 1 20 + 1 30

1 L e q 1 = 1 + 3 + 2 60

1 L e q 1 = 6 60

L e q 1 = 10   m H

Passo 2

Pelo circuito acima, vemos que o indutor equivalente L e q 1 está em série com o indutor de 25   m H . Logo:

L e q 2 = 25 + 10 = 35   m H

Passo 3

Agora, ficamos com apenas dois indutores em paralelo. Logo, vamos calcular a indutância equivalente com aquela velha fórmula do produto das indutâncias sobre a soma delas.

L e q = 35 × 10 35 + 10

L e q = 7,78   m H

Resposta

L e q = 7,78   m H

Exercício Resolvido #8

Introdução à análise de circuitos – Robert L. Boylestad – Ed. 12 – Exercício 11.35

Determine a indutância total do circuito:

Passo 1

A regra de paralelo e série para indutores é a mesma usada com resistores.

Percebemos que s indutores L 4 e L 3 estão em paralelo:

L 6 = 3 * 5,6 3 + 5,6 = 1,95 m H

Passo 2

Essa indutância calculada L 6   está em série com a indutância L 2 :

L 7 =   L 6 +   L 2 = 1,95 + 3,3 = 5,26 m H

Passo 3

Por sua vez, essa indutância L 7 está em paralelo com L 1 :

L 8 = 5,26 * 2,4 5,26 + 2,4 = 1,65 m H

Passo 4

Por fim, a indutância L 8   está em série com L 5 :

L e q = 9,1 + 1,65 = 10,75 m H

Resposta

L e q = 10,75 m H

Exercício Resolvido #9

Livro Sadiku, 5ª edição, p.219, Problema 6.53

Determine a L e q nos terminais do circuito da figura abaixo.

Passo 1

Olhando para o circuito vemos que um indutor de 8   m H está em série com um de 12   m H e um outro de 8   m H está em série com um de 4   m H .

L e q 1 = 8 + 12 = 20   m H

L e q 2 = 8 + 4 = 12   m H

Passo 2

Pelo circuito acima, vemos que o indutor equivalente L e q 1 está em paralelo com o indutor de 5   m H e L e q 2 está em paralelo com o de 6   m H . Logo:

L e q 3 = 5 × L e q 1 5 + L e q 1 = 5 × 20 5 + 20

L e q 3 = 4   m H

L e q 4 = 6 × L e q 2 6 + L e q 2 = 6 × 12 6 + 12

L e q 4 = 4   m H

Passo 3

Agora, temos a associação em série dos dois indutores de 4   m H ligada em paralelo com o indutor de 8   m H .

L e q 5 = 8 ( 4 + 4 )

L e q 5 = 8 × 8 8 + 8

L e q 5 = 4   m H

Passo 4

Agora os três indutores estão em série, é só somar as indutâncias.

L e q = 6 + 4 + 10

L e q = 20   m H

Resposta

L e q = 20   m H

Exercício Resolvido #10

Elaboração própria

Calcule a energia armazenada no circuito de indutores abaixo:

Passo 1

Primeiro devemos calcular a indutância equivalente. Como as duas indutâncias estão em série:

L e q = 3,3 m H + 9,1 m H = 12,4 m H

Passo 2

A fórmula da energia armazenada num indutor é:

w = 1 2 L * I 2

w = 1 2 12,4 m * 5 2 = 0,155 J

Resposta

w = 0,155 J

Exercícios de Livros Relacionados

Em t=0, a tensão em um capacitor de 25 mF é 10 V. Calcule a tensão do capacitor para t0 quando a corrente 5t mA passa através dele.
A corrente em um indutor de 200 mH é i = (B1 cos 200t + B2 sen 200t)e-50t A, t $ 0. A tensão no indutor (convenção passiva) é 4,25 V em t = 0. Calcule a potência nos terminais do indutor em t = 25 ms.
Considere o circuito da figura 6.84. Dado que v t = 12 e - 3 tm V para t0 e i 1 0 = - 10 m A , determine: a i 2 0 ; b i 1 tei 2 t .
No circuito da figura 6.82, i_o (0) = 2 A . Determine i_0 (t) e v_0 (t) para t0 .
Indutores em paralelo podem ser associados da mesma forma que resistores em paralelo.VerdadeiroFalso