20- Determine a série de Fourier para o sinal da Figura . Calcule em , usando os três harmônicos não nulos.
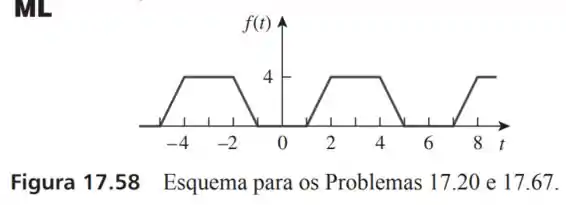
Passo 1
Essa função é uma função par pois :
Nos dando então .
Outra informação que podemos tirar da imagem é que o período dessa onda vale:
Passo 2
Como essa onda é simétrica na vertical podemos fazer duas vezes a integral de metade do trapézio ou seja:
Portanto será:
Passo 3
Agora calculando :
Por integração por partes vemos que:
Logo:
Aplicando todos os intervalos encontramos:
Então teremos a seguinte função de Fourier:
Colocando essa função encontramos:
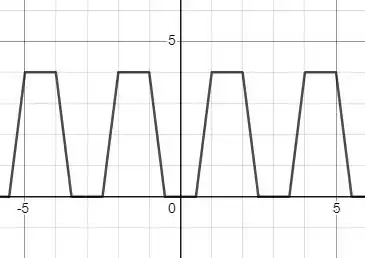
O que diz que estamos certos.
Passo 4
Agora a soma para os três harmônicos nulos:
Isso, é somamos o primeiro, o terceiro e o quinto harmônico.