28- Obtenha a série de Fourier trigonométrica para a forma de onda de tensão mostrada na Figura .
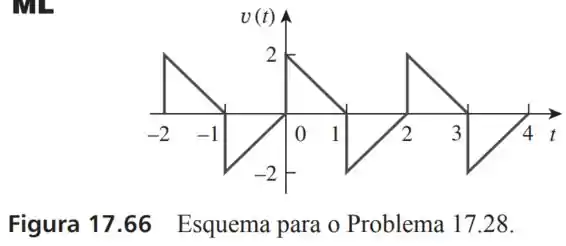
Passo 1
O período dessa onda é de:
Então o será:
E podemos ver que essa onda tem uma simetria de meia onda então:
E por ter simetria de meia onda, nós devemos utilizar somente os pontos ímpares, além de utilizar meio período só no caso vamos usar o intervalo:
Passo 2
Então será:
A integral por partes de será:
Onde para qualquer e
Para ímpar temos:
Passo 3
E será:
Dessa forma:
Onde a integral por partes de será:
Como teremos
Com somente n ímpar.
Então a equação de Fourier dessa função fica:
Nos dando o seguinte gráfico.
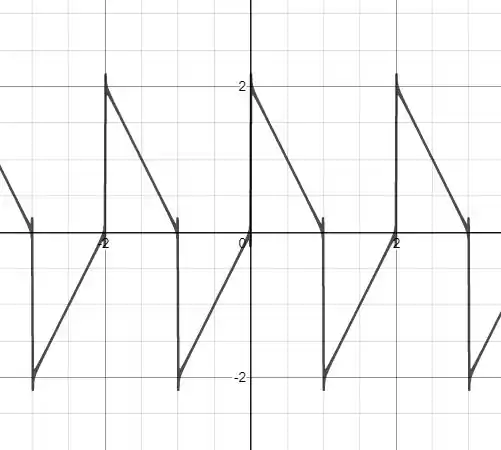
https://www.desmos.com/calculator/a7guojjpt1