Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 57

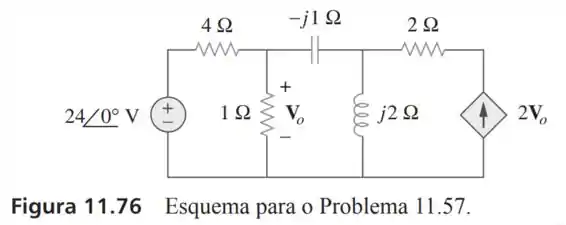
57- Para o circuito da Figura 11.76 , determine as potências média, reativa e complexa pela fonte de corrente dependente.

Passo 1

Vamos redesenhar o circuito de modo a vermos as variáveis intermediárias do sistema:

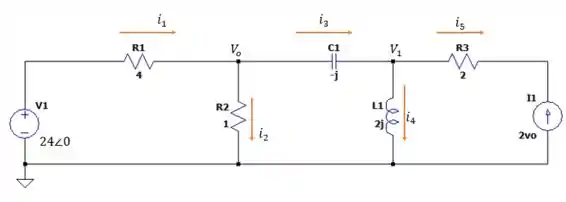
Analisando as correntes que entram e saem do nó V o nós temos:

i 1 = i 2 + i 3

Ou:

24 - V o 4 = V o + V o - V 1 - j

24 - 5 V o 4 = V o - V 1 - j

24 - 5 V o = 4 V o - 4 V 1 - j

24 - 5 V o = 4 V o j - 4 j V 1

24 = V o 5 + 4 j - j 4 V 1

Passo 2

Agora analisando as correntes que entram e saem do nó V 1 temos:

i 3 = i 4 + i 5

V o - V 1 - j = V 1 2 j - 2 V o

2 V o + V o - j = V 1 2 j + V 1 - j

- 2 V o j + V o - j = - V 1 + 2 V 1 - 2 j

V o - 2 j + 1 = V 1 2

V 1 = V o ( 2 - j 4 )

Agora substituindo o V 1 que encontramos e substituindo na equação do passo 1 nós teremos:

24 = V o 5 + 4 j - j 4 V o 2 - j 4

24 = V o 5 + 4 j + V o ( - 8 j - 16 )

24 = V o ( - 11 - j 4 )

V o = - 24 11 + j 4

Dessa forma:

V 1 = - 24 11 + j 4 ( 2 - j 4 )

Passo 3

A tensão em cima da fonte dependente V 2 será a diferença de tensão entre ela e V 1 igual a corrente de 2 v o que passa pelo resistor de 2 Ω :

V 2 - V 1 = 2 × 2 v o

V 2 = 4 v o + V 1 = - 96 11 + j 4 - 24 11 + j 4 ( 2 - j 4 )

V 2 = - 8.202 ∠ - 19.98 - 9.17 ∠ - 83.42 = - 8.76 + j 11.91 = 14.78 ∠ 126.34 °

E a corrente será:

2 v o = - 4 8 11 + j 4 = - 4.1 ∠ - 19.98

Logo a potência complexa será igual a:

S = V I * = 14.78 ∠ 126.34 ° × - 4.1 ∠ 19.98

S = - 60.598 ∠ 146.32 °

S = 50.43 - j 33.604 V A

Ufa

Resposta

S = 50.43 - j 33.604   V A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

49- Determine a potência complexa para os seguintes casos: d ) V R M S = 120 ∠ 30 °V ,Z = 40 + j 60Ω
42- Uma fonte de 110VR M S ,60H z é aplicada a uma impedância de carga Z . A potência aparente entrando na carga é de 120V A com um fator de potência 0.707 atrasado. ( a ) Calcule a potência complexa
44- Determine a potência complexa liberada por v s para o circuito da Figura 11.69 . Seja v s = 100 cos ⁡ 2000 tV .
58- Obtenha a potência complexa liberada para o resistor de 10k Ω da Figura 11.77 a seguir.
62- Para o circuito da Figura 11.81 , determine V_s .