Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 44

A chave no circuito da Figura P7.44 esteve aberta por um longo tempo, antes de ser fechada em t = 0. Determine i 0 ( t ) para t ≥ 0 .

Passo 1

Para t < 0 , o circuito tem a seguinte configuração:

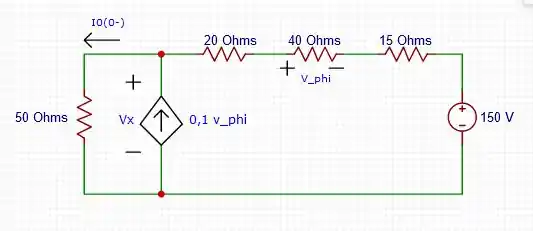
Usando o método dos nós para encontrar v ϕ , temos:

v x 50 - 0,1 v ϕ + v x - 150 75 = 0

Logo,

v ϕ = 40 75 v x - 150

Resolvendo, temos:

v x = 300   V

E

i 0 0 + = v x 50 = 6   A

Passo 2

Para t > 0 a configuração muda completamente, tipo o circuito fica assim:

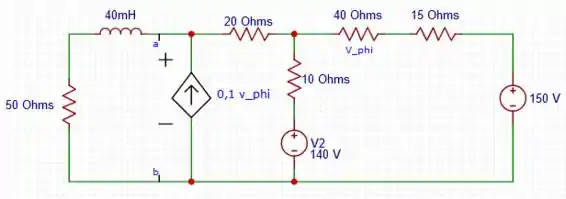
O passo aqui é encontrar a resistência equivalente de Thévenin em relação ao terminal ab, “matando” o indutor e o resistor de 50   Ω , aqui por ter fonte de corrente controlada, temos de usar uma fonte de teste no lugar do indutor e do resistor.

Agora, usa o método dos nós de novo:

- 1 - 0,1 v ϕ + v T - v x 20 = 0

v x - v T 20 + v x 10 + v x 55 = 0  

v ϕ = 40 55 v x

Resolvendo, temos:

v T = 74   V

Então:

R t h = v T 1   A = 74   Ω

Agora é encontrar a tensão com o circuito aberto em relação a (a,b):

- 0,1 v ϕ + v t h - v x 20 = 0

v x - v t h 20 + v x - 140 10 + v x - 150 55 = 0  

Logo,

v ϕ = 40 55 v x - 150

Resolvendo,

v t h = 96   V

Passo 3

O circuito agora devidamente simplificado, fica dessa forma aqui:

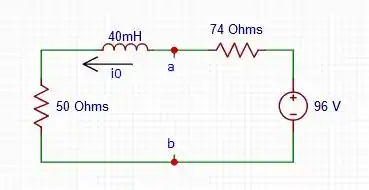
Agora, a corrente depois de muito tempo fica igual a:

i 0 ∞ = 96 124 = 0,774   A

Para a constante de tempo, é usar a fórmula:

τ = 40 × 10 - 3 124 = 0,3226   m s → 1 τ = 3100

E usando a equação geral, encontramos i 0

i 0 = 0,774 + 6 - 0,774 e - 3100 t = 0,774 + 5,226 e - 3100 t   A ,     t ≥ 0  

E finalmente terminamos, ufa! Muita análise para pouca pessoa kkk

Mas até a próxima questão! Vlw!

Resposta

i 0 = 0,774 + 5,226 e - 3100 t   A ,     t ≥ 0  

Exercícios de Livros Relacionados

Para o circuito da Figura 7.98, determine v 0 t quando i 0 = 5 A e v t = 0 .
Determine a constante de tempo para cada um dos circuitos da figura 7.96.
No circuito da Figura 7.99 , determine i t para t0 se i 0 = 6 A .
No circuito da figura 7.10, determine o valor de R para o qual a energia em regime estacionário armazenada no indutor seja 1 J .
No circuito da figura 7.93, v t = 80 ⋅ e - 10 3 tV , t0 i t = 5 ⋅ e - 10 3 tm A , t0 a Determine R , Leτ . b Calcule a energia dissipada na resistência para 0t0.5 m s .