No circuito da figura 7.10, determine o valor de para o qual a energia em regime estacionário armazenada no indutor seja .
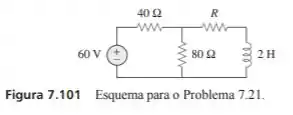
Passo 1
Vamos, primeiramente, calcular as “medidas” de Thevenin (tensão e resistência) para que logo após consigamos encontrar a expressão para a corrente e, por fim, encontrarmos o valor de que é o que desejamos de fato. Dessa forma, temos para a tensão de thevenin um divisor de tensão dado por
Agora, conseguimos uma expressão para tendo em vista que
Passo 2
Temos, por fim, como encontrar o valor de aplicando a equação da energia para um indutor que é dada por
Como só nos importa a solução positiva, tendo em vista que estamos falando do valor de um resistor, podemos tirar a raíz quadrada dos dois lados e obteremos