Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 68

Determine os circuitos equivalentes de Thévenin e de Norton nos terminais a-b no circuito da Figura 10.110.

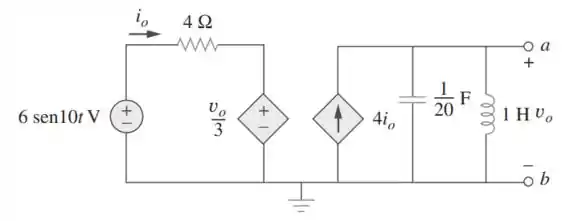
Passo 1

Vamos lá galera! Primeiro, temos que transformar os componentes que estão no domínio do tempo e transformar para o domínio da frequência. Fazemos isso para possibilitar os cálculos!

Nós primeiro vamos achar a tensão de Thevenin usando o circuito abaixo!

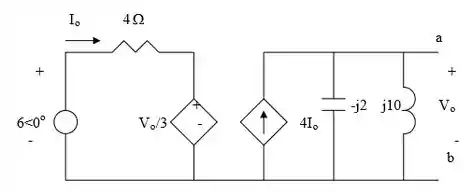
Passo 2

Para esse circuito, temos que:

j 10 | | - j 2 = j 10 - j 2 j 10 - j 2 = - j 2.5

v o = 4 I o × - j 2.5 = - j 10 I o

- 6 + 4 I o + 1 3 V o = 0

Combinando essas equacoes para acharmos I o , temos:

I o = 6 4 - j 10 / 3 ,     V T h = V o = - j 10 I o = - j 60 4 - j 10 3 = 11.52 ∠ - 50.19 °

Portanto,

V T h = 11.52   s e n   ( 10 t - 50.19 ° )

Passo 3

Para achar a impedância de Thevenin, vamos inserir uma fonte de corrente de 1 A nos terminais a-b.

4 I o + 1 3 V o = 0 → I o = - V o 12

1 + 4 I o = V o - j 2 + V o j 10

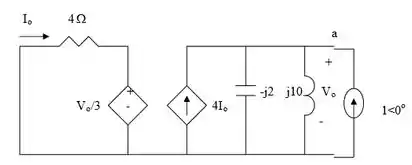
Combinando novamente, essas equações,

V o = 1 0.333 + j 0.4 = 1.2293 - j 1.4766   V

Logo, para esse caso,

Z T h = V o 1 = 1.2293 - j 1.477   Ω

Resposta

V T h = 11.52   s e n   ( 10 t - 50.19 ° )

Z t h = 1.2293 - j 1.477   Ω

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o circuito fasorial correspondente ao Ex. 11.2.3, troque a parte à esquerda dos terminais a - b pelo equivalente de Thévenin e calcule a corrente i 1 em regime permanente.
Use a análise nodal para calcular o valor de v em regime permanente, se v g = V m cos ⁡ ω t e calcule a amplitude de v para os casos de ω = (a) 0 , (b) 1000 e (c) 10 6 rad/s. Compare o resultado para
Calcule a tensão v em regime permanente, usando análise nodal.
Calcule a corrente i em regime permanente.
Calcule a tensão v em regime permanente.