Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 20
A fonte de 240 V, e resistência interna de 2 V, no circuito da Figura P7.20, sofre inadvertidamente um curto-circuito em seus terminais a,b. No instante em que a falha ocorre, o circuito estava em funcionamento havia um longo tempo. a) Qual é o valor inicial da corrente i ab de curto-circuito entre os terminais a,b? b) Qual é o valor final da corrente i ab? c) Em quantos microssegundos, depois de o curto-circuito ter ocorrido, a corrente de curto atinge 114 A?
Passo 1
[a] – Nesse caso, o circuito se comportará da seguinte forma:
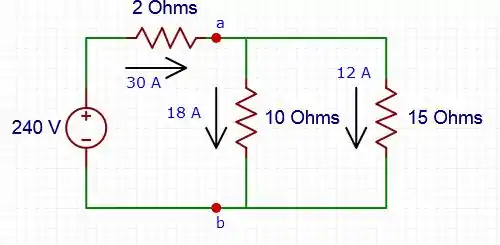
Lembre-se, indutores se comportam como curto depois de muito tempo em um estado de estabilidade (ou seja, uma corrente contínua) e como circuito aberto em transições “rápidas” como funções degrau, rampa e et cetera.
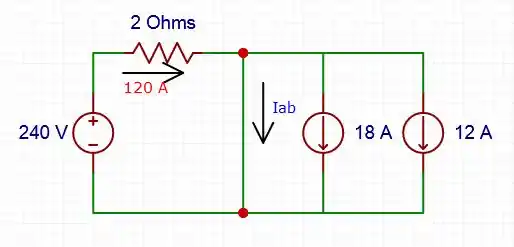
Passo 2
[b] -
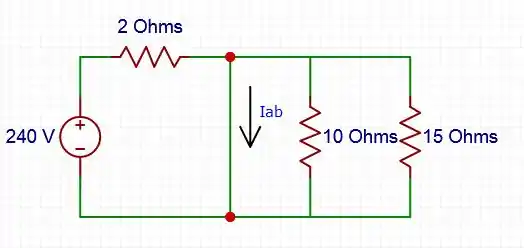
A corrente sempre escolher o local que se tenha menos resistência, e no curto entre a e b seria o ideal para ela. Com isso, pelos resistores não passam corrente, então:
Passo 3
[c] - O circuito se comportará da seguinte maneira:
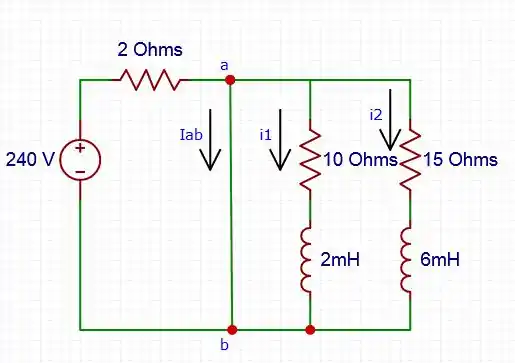
Com isso, podemos calcular e :
Já se tendo as informações das correntes iniciais e das constantes de tempo, então já se pode substituir na fórmula de , dessa forma:
E para :
No caso de , temos aquela equação que já tinha sido encontrada na letra a (essa aqui , logo, passando para um momento de instante de tempo qualquer, temos a equação:
Isso parece ser algo conhecido e fácil de ser resolvido, então fazendo a substituição, podemos obter: