Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 71

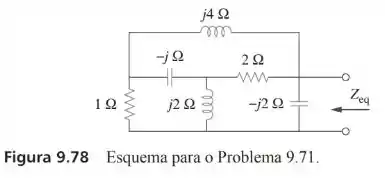
Obtenha a impedância equivalente para o circuito da Figura 9.78.

Passo 1

Para facilitar nossa interpretação vamos utilizar a transformação y - d e l t a   e, assim, obteremos o seguinte circuito mais simples (em termos de análise de impedância equivalente)

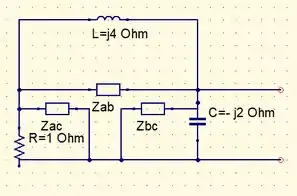
Assim, vamos calcular as impedâncias nomeadas primeiramente obtendo então

Z a - b = 2 - j 2 + j 4 j 2 = 2 + j 2 j 2 = 1 - j

Z a - c = 2 + j 2 2 = 1 + j  

Z b - c = 2 + j 2 - j = - 2 + j 2

A impedância mais superior no gráfico ( j 4   Ω   ) está em paralelo com Z a b e o equivalente vai ser dado por

j 4 | | Z a b = j 4 ⋅ 1 - j 1 + j 3 = 1.6 - j 0.8

Temos também o resistor de 1 Ω em paralelo com Z a c   e o equivalente vai ser dado por

1 | | Z a c = 1 ⋅ 1 + j 2 + j = 0.6 + j 0.2

Essas duas impedâncias equivalente estão associadas em série, assim, vamos obter

j 4 Z a b + 1 Z a c = 1.6 - j 0.8 + 0.6 + j 0.2 = 2.2 - j 0.6

Pronto, agora temos tudo o que é necessário para encontramos e impedância equivalente total do circuito fazendo

1 Z e q = 1 - j 2 + 1 - 2 + j 2 + 1 2.2 - j 0.6 = j 0.5   -   0.25   -   j 0.25   +   0.4231 + j 0 . 1154  

1 Z e q = 0.173 + j . 0.3654 ≈ 0.4043 ∠ 64.66 °

∴ Z e q = 2.473 ∠ - 64.66 °   Ω = 1.058 - j 2.235   Ω

Resposta

Z e q = 2.473 ∠ - 64.66 °   Ω = 1.058 - j 2.235   Ω

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

60- Obtenha Z e n t para o circuito da Figura 9.67
61- Determine Z e q no circuito da Figura 9.68 .
59- Para o circuito da Figura 9.66 , determine Z e n t . Considere ω = 10r a d / s
65- Determine Z T e I no circuito da Figura 9.72 .
64- Determine Z T e I no circuito da Figura 9.71