Resolva a equação:
Solução
Observemos que a equação só tem solução para
Como
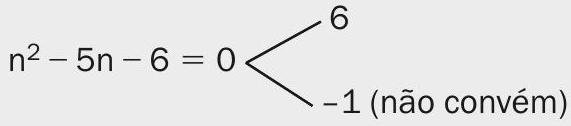
o conjunto solução é {6}.
Como

o conjunto solução é {6}.
Passo 1
O enunciado pede para resolver a equação
onde
e resolver para
Passo 2
Pela definição de arranjo simples, temos
Substituindo na equação dada, obtemos
Passo 3
Como estamos buscando soluções com
Passo 4
Expandindo o produto e levando tudo para um lado, resulta
Aplicando a fórmula de Bhaskara, o discriminante é
portanto as raízes são
isto é,
Passo 5
Verificando a condição
Resposta
O conjunto-solução é