Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 57

Considere o campo de velocidade estacionário, incompressível e bidimensional do Problema 4-55. Usando os resultados do Problema 4-55 ( a ) faça o seguinte:

( a ) Da definição fundamental de taxa de deformação por cisalhamento (metade da taxa de diminuição do ângulo entre duas retas inicialmente perpendiculares que se interceptam em um ponto), calcule a taxa de deformação por cisalhamento ε x y no plano x y . (Sugestão: Use os lados inferior e esquerdo da partícula de fluido, que se cruzam a 90 ° no canto inferior esquerdo da partícula no instante inicial.)

( b ) Compare seus resultados com aqueles obtidos pelas equações para ε x y em coordenadas cartesianas, ou seja

ε x y = 1 2   ∂ u ∂ y + ∂ v ∂ x

Passo 1

Para resolução da questão ( a ) iremos precisar da taxa de tensão de cisalhamento, que pode ser expressa como sendo:

ε x y = 1 2 ∂ u ∂ y + ∂ v ∂ x

A partir da definição fundamental da taxa de deformação por cisalhamento no plano x - y , consideramos a borda inferior e a borda esquerda da partícula fluida, que se cruzam a 90 ° no canto inferior esquerdo no momento t .

Passo 2

Definimos o ângulo α entre a borda inferior e a borda esquerda da partícula fluida e o ângulo β , o complemento de α como pode-se notar na figura abaixo.

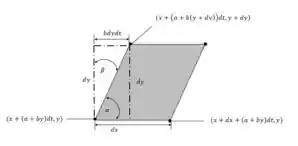
Passo 3

A taxa de diminuição do ângulo α   ao longo do intervalo de tempo d t é obtida a partir da aplicação da trigonometria. Primeiro devemos calcular o ângulo β ...

 n g u l o   β   n o   t e m p o   t   +   d t :

β = arctan ⁡ b d y d t d y = arctan ⁡ b d t ≈ b d t                 ( 2 )

A aproximação é válida para ângulos muito pequenos. Como o intervalo de tempo d t   →   0 , portanto nossa equação 2 está correta.

 n g u l o   α   n o   t e m p o   t   +   d t :

α = π 2 - β ≈ π 2 - b d t                         ( 3 )

Durante esse intervalo de tempo,   α muda de 90 °   π 2   r a d i a n o s para a expressão dada pela acima.

Passo 4

Assim, a taxa de variação de α se torna:

d α d t = 1 d t π 2 - b d t ⏟ α   e m   t + d t - π 2 ⏟ α   e m   t = - b                         ( 4 )

Por fim, como a taxa de deformação por cisalhamento é definida como metade da taxa de diminuição do ângulo α , temos que:

ε x y = - 1 2 d α d t = b 2                   ( 5 )

( b ) Portanto da equação 1, podemos obter a seguinte formulação:

ε x y = 1 2 ∂ u ∂ y + ∂ v ∂ x = 1 2 b + 0 = b 2                 ( 6 )

Ambos os métodos para obter a taxa de deformação por cisalhamento concordam (Eq. 5 e Eq. 6).

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o escoamento de Poiseuille bidimensional do problema 4 - 79 . O fluido entre as placas é água a 40° C . Seja h = 1,6m m a altura da lacuna e d P / d x = - 230N / m 3 o gradiente de pressão.
O escoamento de duto convergente é modelado pelo campo de velocidade em regime permanente e bidimensional do Problema 4-15. Use a taxa de deformação volumétrica para verificar se esse campo de escoame
Usando os resultados do Problema 4-58: ( a ) Esse escoamento é rotacional ou irrotacional? ( b ) Calcule a componente z da vorticidade para esse campo de escoamento.
Para o campo de velocidade do Problema 4-49, calcule o vetor vorticidade. Em qual direção aponta o vetor vorticidade?
Uma equação geral para um campo de velocidade bidimensional e em regime permanente que é linear nas direções espacial ( x e y ) é V → = u , v = U + a 1 x + b 1 y i → + ( V + a 2 x + b 2 y ) j → Onde U