Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 11.Problemas - Ex. 17
17 – Considere um trocador de calor de tubo concêntrico com uma área de 60 m2 operando sob as seguintes condições:
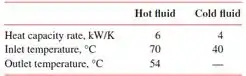
A) Determine a temperatura de saída do fluido frio.
B) O trocador de calor está operando com escoamento contracorrente ou paralelo, ou não pode dizer nada sobre o escoamento com as informações disponíveis?
C) Calcule o coeficiente global de troca térmica.
D) Calcule a efetividade deste trocador de calor.
E) Qual seria a efetividade deste trocador de calor se seu comprimento fosse muito maior?
Passo 1
A)
Para determinarmos a temperatura de saída do fluido frio, basta fazermos o seguinte balanço de energia. A quantidade de calor transferido do fluido quente para o fluido frio é exatamente igual ao calor removido do fluido quente, assim
Onde,
Assim,
Passo 2
Vamos isolar Tf,s
Aplicando os valores:
Passo 3
B)
Para responderemos a pergunta do item B, vamos primeiro relembrar as características intrínsecas a cada padrão de escoamento, contracorrente e paralelo.
Em um trocador de calor com padrão de escoamento em paralelo, a temperatura do fluido frio na saída nunca pode ultrapassar a temperatura do fluido quente na saída, pois para esse tipo de escoamento, o limite é que a temperatura do fluido quente seja igual temperatura do fluido frio na saída do trocador.
Já para um padrão de escoamento em contracorrente, a temperatura do fluido frio na saída pode ser maior do que a temperatura do fluido quente na saída, devido ao fato de que o ponto de saída do fluido frio é o ponto de entrada do fluido quente que está em uma temperatura bem mais elevada do que na sua saída.
Logo, com base nesses conceitos e no resultado obtido, pode-se dizer que o trocador de calor está operando em contracorrente, pois obteve-se uma temperatura de saída do fluido frio maior do que a temperatura de saída do fluido quente.
Passo 4
C)
Para determinarmos o coeficiente global de troca térmica, U, podemos usar simplesmente o método da efetividade-NTU.
O parâmetro NTU é definido como:
Onde, Cmin é o menor valor entre as taxas de capacidades calorificas que para este caso é
O valor de NTU pode ser determinado pela Tabela 11.4 do Incropera, pegando a correlação apropriada para este caso, que será a correlação para um trocador de calor bitubular com escoamento em contracorrente. Pela Tabela 11.4:
Onde,
Passo 5
A efetividade, ε é determinado pela seguinte equação
Assim,
Sendo,
Assim,
Aplicando os valores:
Passo 6
Calculando NTU:
Aplicando os valores:
Passo 7
Calculando o coeficiente global de troca térmica:
Isolando U
Aplicando os valores:
Passo 8
D)
Como já calculado que a efetividade é:
Passo 9
E)
Para um trocador de calor com um comprimento muito maior, ou seja, uma área de troca térmica muito maior, a temperatura do fluido frio na saída se aproximaria muito da temperatura de entrada do fluido quente, assim pela expressão que definimos anteriormente para a efetividade
Para o qual para uma área muito grande, tendendo ao infinito por exemplo, teremos que
Assim, a efetividade será
Resposta
A)
B)
O trocador de calor está operando em contracorrente, pois obteve-se uma temperatura de saída do fluido frio maior do que a temperatura de saída do fluido quente.
C)
D)
E)