Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 137

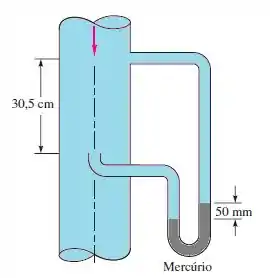
Para o escoamento de água a 20°C na figura abaixo, use a combinação de tubo de Pitot e tomada de pressão estática para calcular (a) a velocidade na linha de centro e (b) a vazão volumétrica no tubo liso de 125 mm de diâmetro. (c) Que erro será cometido na vazão se a diferença de elevação de 30,5 cm for desprezada?

Passo 1

E ai, galera! Tranquilidade? Bora que bora encarar mais um desafio?

Vamos pegar as propriedades da água na temperatura dada!!

ρ = 998   k g / m ³

μ = 0,001 k g m . s

Bem, para o manômetro dar 50 mm ali na altura, precisamos usar nossa velha e boa hidrostática.

p o B - p A = ρ H g - ρ á g u a g h + ρ á g u a g   h '

Onde h’ representa exatamente a altura de água que está dentro do tubo, ou seja, 30,5 cm!

Bem, então primeira coisa que vamos fazer é: vamos abrir essa densidade do mercúrio porque ela não foi dada de forma direta, mas podemos obter em uma tabela sua densidade relativa.

p o B - p A = d - 1 ρ á g u a g h + ρ á g u a g h '

Passo 2

Note que dentro do tubo temos um escoamento, então precisamos aplicar um balanço de energia ali para saber qual é a diferença de pressão entre o ponto A e B.

p B - p A = ρ á g u a g h ' - ρ á g u a g h f - A B

Ou seja, a diferença de pressão é causada pela diferença entre a pressão hidrostática na coluna (que contribui de forma positiva), mas tem que ser descontada o quanto é perdido durante esse “caminho” que o fluido usa para escoar. Note que, necessariamente p B < p A para que o escoamento esteja na direção mostrada na figura. Mas como não gostamos muito de trabalhar com sinais negativos, vamos inverter:

p A - p B = ρ á g u a g h f - A B - ρ á g u a g h '

Portanto, nossa equação pode tomar a seguinte forma:

p o B - p B = d - 1 ρ á g u a g h m a n o + ρ á g u a g h f - A B

Onde h f - A B = f L D V 2 2 g

Passo 3

Ao substituir os valores de cada um dos parâmetros, você observará que:

ρ H g - ρ á g u a g h m a n o = 6224   P a

ρ á g u a g h f - A B = ? ?

Vamos aproximar inicialmente o valor de queda de pressão como sendo em torno de 6224 Pa, e assim obter qual será a velocidade no centro do meu escoamento:

V C L = 2 Δ p ρ 1 2 = 2 6224 998 1 2 = 3,53   m / s

Portanto, a velocidade média é dada como sendo 85% da velocidade no centro, o que diz que:

V m é d i a = 0,85 V C L = 3   m / s

Logo,

R e = ρ V m é d i a D μ = 998 3 0,125 0,001 = 381500

Observando qual é o valor do fator de atrito para tubos lisos no diagrama de Moddy para esse valor de Re, f = 0,0138.

Δ p = f L D ρ V m é d i a 2 2 = 153   P a

Passo 4

Se a gente agora corrigir a diferença de pressão lida no tubo de Pitot como sendo:

Δ p p i t o t = 6224 + 153 = 6377   P a

Podemos então agora fazer iterações e convergir rapidamente para o valor final, ou seja, colocamos agora esse novo valor dentro da equação de V C L , encontramos depois uma nova velocidade média, calculamos Re e obtemos um valor f para tubos lisos no diagrama de Moddy. Com isso, recalculamos todo o valor de Δ p p i t o t e fazemos os cálculos novamente até convergir.

  1. Consideramos um valor inicial de Δ p
  2. Calculamos VCL
  3. Calculamos Vmédia
  4. Calculamos Re
  5. Obter f no diagrama de Moody para tubos lisos
  6. Calcular Δ p h f = f   L D ρ V m é d i a 2 2
  7. Recalcular Δ p
  8. Voltar ao passo 2 até convergência

Ao final temos os seguintes valores:

  1. e (b)

f = 0,01375

V C L = 3,6   m / s

V m é d i a = 0,85 V C L = 3,06   m / s

Q = π 4 D 2 V m é d i a = 0,04   m 3 / s

Passo 5

(c) O erro comparado com o nosso valor estimado anteriormente de 3 m/s é no entorno de 2%

Resposta

a V m é d i a = 3,06   m / s

b Q = 0,04 m 3 s

c   E r r o = 2 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

8.193Águaa65°Cescoaatravésdeumorifíciocomdiâmetrode75mminstaladoemumtubode150mmdediâmetrointerno.A vazãoé20L/s.Determineadiferençadepressãoentreastomadasdecanto.
8.195Ummedidorventuri,com76,2mmdediâmetronagarganta,éinstaladoemumalinhade152mmdediâmetroquetransporta águaa24ºC.Aquedadepressãoentreatomadademontanteeagargantadoventurié305mmdemercúrio.Calculeavazão.
8.203Canudinhosderefrigerantepodemserusadosparamelhoraroescoamentodearemumexperimento.Opreenchimentodeum trechodotubocomcanudos,demodoaformarum“elementodeescoamentolaminar”,poderiapermitiramediçãodire
Um orifício de borda-viva, com tomadas de canto, e um manômetro de coluna de água são usados para medir vazão de ar comprimido. Os seguintes dados são disponíveis:Calcule a vazão em volume na linha, e
Considere a instalação de um bocal medidor em um tubo. Aplique as equações básicas ao volume de controle indicado, para mostrar que a perda de carga permanente através do medidor pode ser expressa, em