PA11.3 – Reconsidere o Problema P6.77 como um exercício de seleção de turbinas. Selecione um tamanho e uma rotação de rotor da família de turbinas Francis da Figura 11.22d para fornecer uma potência máxima gerada pela turbina. Calcule a potência de eixo da turbina e observe a natureza prática do seu projeto.

Figura 11.22d

Vamos relembrar, então, os coeficientes adimensionais, que são eles definidos por

Onde,

-CQ é o coeficiente de vazão;

-Q é a vazão volumétrica do fluido;

-CH é o coeficiente de altura de queda;

-CP é o coeficiente de potência;

-g é constante da gravidade, 9,81 m/s2;

-ρ é a massa especifica (densidade) da água, 998 kg/m3;

-n é a rotação, em rps;

-Pe é a potência de eixo gerada pela turbina;

-H é a altura de queda da turbina.

Pela figura 11.22d, vemos que os valores de cada coeficiente, correspondente ao ponto ótimo (máximo rendimento) são

Onde, os coeficientes com (*) significam que são os valores dos coeficientes no ponto de máximo rendimento da turbina; e ηmáx é o rendimento máximo.

Pelas expressões dos coeficientes, , vemos que não é possível explicitar D ou n sem colocar um em função do outro, então teremos que pegar duas equações para resolver.

Pegando a Eq. de CQ*

Isolando n

Pegando agora a expressão de CH*

Substituindo a Eq1 na equação de CH*

Isolando D

Não temos o valor da altura de queda, H, mas podemos acha-lo pelo Equação de Bernoulli

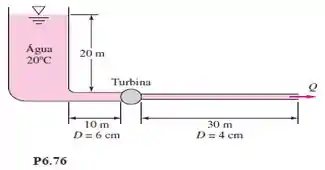
Relembrando da Eq. de Bernoulli, esta é referente a um balanço de energia mecânica entre dois pontos, que leva em consideração as variações de energia cinética, potencial e energia de pressão nesses dois pontos, além também da perda de energia por atrito. No volume de controle da figura P6.76, vemos que temos uma turbina, então relembrando da equação de Bernoulli aplicada para processos com máquinas de fluxo, também devemos ter um termo referente a energia da turbina. A expressão é

Onde,

-H é a altura de queda, que é a energia disponível no fluido para fornecer a turbina;

-Δp é a variação de pressão do sistema;

-ΔV2 é a variação de energia cinética do sistema;

-Δz é a variação de energia potencial do sistema;

-hLT é a perda de carga total do sistema, devido ao atrito do fluido com a tubulação e ao atrito com os acessórios;

-ρ é a densidade do fluido;

-g é a constante da gravidade, g=9,81 m/s2.

Para hLT

Onde,

-hp e hac são a perda de carga devido ao atrito do fluido com a tubulação e a perda de carga devido ao atrito com os acessórios, respectivamente;

Aplicando o balanço de energia mecânica (Eq de Bernoulli) entre o reservatório (1) e a saída da tubulação (2), da figura P6.76, lá em cima no enunciado

Onde,

-p1 e p2 são a pressão no reservatório de baixo e no de cima, respectivamente;

-V1 e V2 são a velocidade do fluido no reservatório de baixo e no de cima, respectivamente;

-z1 e z2 são a altura no nível no reservatório de baixo e no de cima, respectivamente;

-hp é a perda de carga por atrito do fluido na tubulação;

-ρ é a densidade da água, ρ=998 kg/m3;

-g é a constante da gravidade, g=9,81 m/s2.

Na Eq1 não foi adicionado o termo hac, pois podemos desprezar as perdas localizadas, isto é, as perdas com acessórios, sendo esta pouca significante para os cálculos.

Isolando H

Vamos agora analisar a figura P6.76, lá em cima para ver quem é quem da equação de Bernoulli.

Analisando o esquema da figura P6.76, lá em cima, vemos que

Onde, patm é a pressão atmosférica que você pode considerar para as duas pressões, pois os dois reservatórios estão abertos para a atmosfera.

Já para as alturas z1 e z2, temos pela figura que

Também vemos que para V1, nós podemos considerar esta nula, pois a velocidade do fluido no ponto 1, que é no topo do reservatório, é muito pequena em relação a V2, devido ao tamanho do reservatório. Podemos demonstrar isso pela equação da continuidade

Onde,

-D1 e D2 são, respectivamente, o diâmetro do reservatório (DReserv) e o diâmetro do injetor (Dj);

Isolando V1

Como você pode ver pela figura P11.95 o tamanho do reservatório é muito maior do que a abertura do injetor, assim

Com isso, o termo dos diâmetros

Consequentemente,

Assim, a eq. da altura de queda, H, agora é

Pela equação de Darcy-Weisbach podemos determinar a perda de carga, hp

Onde,

-hp é a perda de carga por atrito na tubulação;

-f é o fator de atrito;

-LT é o comprimento total da tubulação;

-DT é o diâmetro interno da tubulação;

-V é a velocidade do fluido na tubulação;

-g é a constante da gravidade, g=9,81 m/2.

Vamos voltar a figura 6.76. Nela você vai ver que a tubulação da sucção da turbina (tubo do lado esquerdo) e do lado direito possuem diâmetros diferentes. Isso significa que você vai ter que dividir a perda de carga na tubulação, hp, em duas.

Onde,

-hp,Total é a perda de carga total por atrito na tubulação;

-fEsq e fDir são, respectivamente, o fator de atrito na tubulação do lado esquerdo da turbina e da tubulação do lado direito;

-LT,Esq e LT,Dir são, respectivamente, o comprimento da tubulação do lado esquerdo da turbina e do lado direito;

-DT,Esq e DT,Dir são, respectivamente, o diâmetro interno da tubulação do lado esquerdo da turbina e do lado direito;

-VEsq e VDir são, respectivamente, a velocidade do fluido na tubulação do lado esquerdo da turbina e do lado direito da turbina;

A velocidade do lado direito é igual a velocidade 2, V2

A velocidade da esquerda, VEsq, se relaciona matematicamente com V2 pela equação da continuidade

Sendo então

Substituindo as expressões de perda de carga na Eq4

Calculando a velocidade do fluido na saída da tubulação, V2

Podemos usar a seguinte relação entre vazão e velocidade de escoamento

Onde,

-Q é a vazão volumétrica;

-A é a área da seção transversal do tubo;

-V é a velocidade do fluido.

A área de seção transversal é função do diâmetro da tubulação

Assim,

Isolando V

Pelo problema 6.77

Convertendo a vazão para m3/s

Aplicando os valores

Vamos agora determinar o fator de atrito f.

O fator de atrito depende de Reynolds e da rugosidade relativa

A Eq. de Reynolds é

Onde,

-Re é o número de Reynolds;

-ρ é a densidade do fluido (água), ρ=998 kg/m3 para a água;

-DT é o diâmetro da tubulação;

-V é a velocidade de escoamento do fluido;

-μ é a viscosidade dinâmica do fluido (água), μ=0,001 kg/m.s para a água;

Como já sabemos

Assim,

Calculando os Re’s

Pelo problema 6.77, o tubo é de ferro forjado e para este material a rugosidade, ε, vale

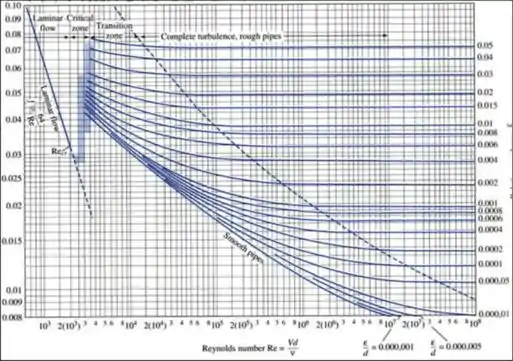
Usando a diagrama de Moody

Calculando a altura de queda, H, pela Eq5

Aplicando os valores

Agora com o valor de H podemos calcular o diâmetro do rotor pela Eq2

Aplicando os valores

Agora vamos voltar na Eq1 e achar n

Aplicando os valores

Em rpm

Calculando a potência de eixo gerada pela turbina.

Podemos calcula-la pela expressão do coeficiente de potência

Isolando Pe

Aplicando os valores