Processos em batelada são frequentemente usados em operações químicas e farmacêuticas para atingir uma desejada composição química do produto final. Os processos de transferência de calor presentes são tipicamente transientes, envolvendo um líquido com volume fixo que pode ser aquecido da temperatura ambiente até uma temperatura especificada pelo processo ou resfriado da temperatura do processo para a temperatura ambiente. Considere um processo em batelada no qual um fármaco (o fluido frio, ) é despejado em um vaso isolado termicamente e fortemente agitado (um reator de mistura ideal) e aquecido pela passagem de um fluido quente () através de uma serpentina submersa, de parede delgada e área superficial . A vazão mássica, , a temperatura de entrada média, , e o calor específico, , do fluido quente são conhecidos, como o são a temperatura inicial, , o volume, , a massa específica, , e o calor específico, , do fármaco. A transferência de calor do fluido quente para o fármaco é governada por um coeficiente global de transferência de calor .

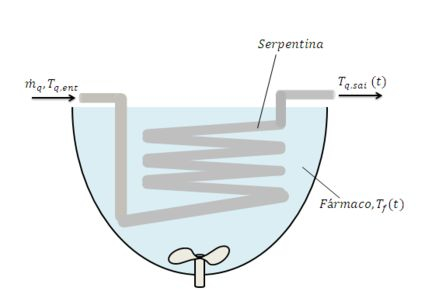
(a) Partindo de princípios básicos, deduza expressões que possam ser usadas para determinar as variações de e com o tempo durante o processo de aquecimento.

(b) Seja um volume de fármaco , com uma massa específica , calor específico e uma temperatura inicial de . Uma serpentina com comprimento , diâmetro do tubo e diâmetro da serpentina está submersa no vaso. O fluido quente é alimentado na serpentina a e auma vazão de . O coeficiente convectivo na superfície externa da serpentina pode ser aproximado por e as propriedades do fluido quente são , , e . Para as condições anteriores, calcule e represente graficamente a temperatura do fármaco e a temperatura de saída do fluido quente como uma função do tempo para o intervalo . Quanto tempo demora para se atingir uma temperatura da batelada de ? O operador do processo pode controlar o tempo de aquecimento variando . Para , explore o efeito da vazão mássica no tempo necessário para atingir um valor de .

Como dissemos anteriormente, a taxa de transferência de calor também pode ser expressa como a energia perdida pelo fluido quente ao longo do escoamento:

Igualando esta expressão com a anterior:

E temos uma expressão para a temperatura de saída do fluido quente. Vamos agora obter uma expressão para a temperatura do fármaco.

Assim como expressamos a taxa de transferência de calor em termos do calor perdido pelo fluido quente, também podemos escrevê-la como a energia recebida pelo fármaco. Então:

Igualando com a expressão em função do fluido quente:

Substituindo a relação de :

Integrando dos dois lados:

E chegamos em uma função da temperatura do fármaco que depende do tempo de processo.

Vamos agora para o item (b). Neste item recebemos alguns dados de propriedades do fluido quente e do fármaco, bem como das dimensões da serpentina. Devemos agora utilizar estas informações nas relações que encontramos no item (a) para graficar as temperaturas do fármaco e da saída de fluido quente, ao longo do intervalo . Vamos lá?

Como primeiro passo antes de utilizar as nossas expressões ainda temos uma variável para obter: o coeficiente global. Como a serpentina tem parede delgada, podemos considerar que as áreas de troca térmica interna e externa são praticamente iguais. Neste caso, o coeficiente global se reduz à:

Sabemos que pelo enunciado mas ainda precisamos calcular o valor do coeficiente de convecção externo.

Para isso, começamos calculando o número de Reynolds:

Como , o regime de escoamento é turbulento.

Para regime turbulento no interior de dutos cilíndricos:

E o coeficiente global será:

Com o auxílio de Excel, ou outra ferramenta gráfica, iremos aplicar este valor nas expressões de temperatura do fármaco e temperatura de saída do fluido quente e, então fazer o gráfico destas funções para valores de tempo no intervalo :

E

Aplicando estas funções para diversos valores de tempo no intervalo devemos obter curvas parecidas com:

Ainda no item (b), devemos verificar em quanto tempo a temperatura do fármaco atinge . Substituindo este valor na expressão:

Achou que tinha acabado? Então respira fundo porque ainda tem mais uma coisa a se fazer. Recebemos a informação de que é possível alterar a vazão mássica de fluido quente. Sabendo disso, devemos verificar como a vazão influencia no tempo necessário para atingir . Vamos lá?

Se alteramos a vazão isto irá influenciar no número de Reynolds e, por consequência, no valor de e do coeficiente global. Para ver como isto influencia no tempo de processo, vamos fazer os cálculos para os dois extremos de vazão: e .

Começando com a vazão mínima, o número de Reynolds será:

Como , o regime de escoamento é turbulento.

Para regime turbulento no interior de dutos cilíndricos:

E o coeficiente global será:

Aplicando este valor na expressão de temperatura do fármaco:

Fazendo agora para a vazão máxima, o número de Reynolds será:

Como , o regime de escoamento é turbulento.

Para regime turbulento no interior de dutos cilíndricos:

E o coeficiente global será:

Aplicando este valor na expressão de temperatura do fármaco:

Então, como esperado, um aumento na vazão de fluido quente aumenta a turbulência do escoamento, gerando um coeficiente global de maior valor e uma troca térmica mais eficiente. Portanto, aumentando a vazão de fluido quente é possível diminuir o tempo de processo.